Предмет: Алгебра,
автор: viToriaD
установіть відповідність між функціями (1-4) та їх похідними (а-д)
Допоможіть!!!!
Приложения:
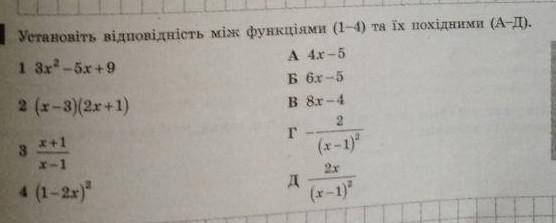
Ответы
Автор ответа:
5
Установить соответствие между функциями f(x)=3x^2-5x+9; f(x)=(x-3)(2x+1); f(x)=(x+1)/(x-1); f(x)=(1-2x)^2 и их производными.
Ответ:
1Б 2А 3Г 4В
Объяснение:
Формулы нахождения производных, которые будут использоваться:
где х - переменная, с - постоянная.
- f(x)=3x^2-5x+9
1Б - f(x)=3x^2-5x+9 -> f'(x)=6x-5
- f(x)=(x-3)(2x+1)
2A - f(x)=(x-3)(2x+1) -> f'(x)=4x-5
- f(x)=(x+1)/(x-1)
3Г - f(x)=(x+1)/(x-1) -> f'(x) = -(2/(x-1)^2))
- f(x)=(1-2x)^2
4B - f(x)=(1-2x)^2 -> f'(x)=8x-4
Похожие вопросы
Предмет: Русский язык,
автор: ruzvelt3000
Предмет: Русский язык,
автор: dashsdykins11
Предмет: Українська мова,
автор: vladislavkhavr
Предмет: Українська література,
автор: anastasia3950
Предмет: Химия,
автор: Alegraja