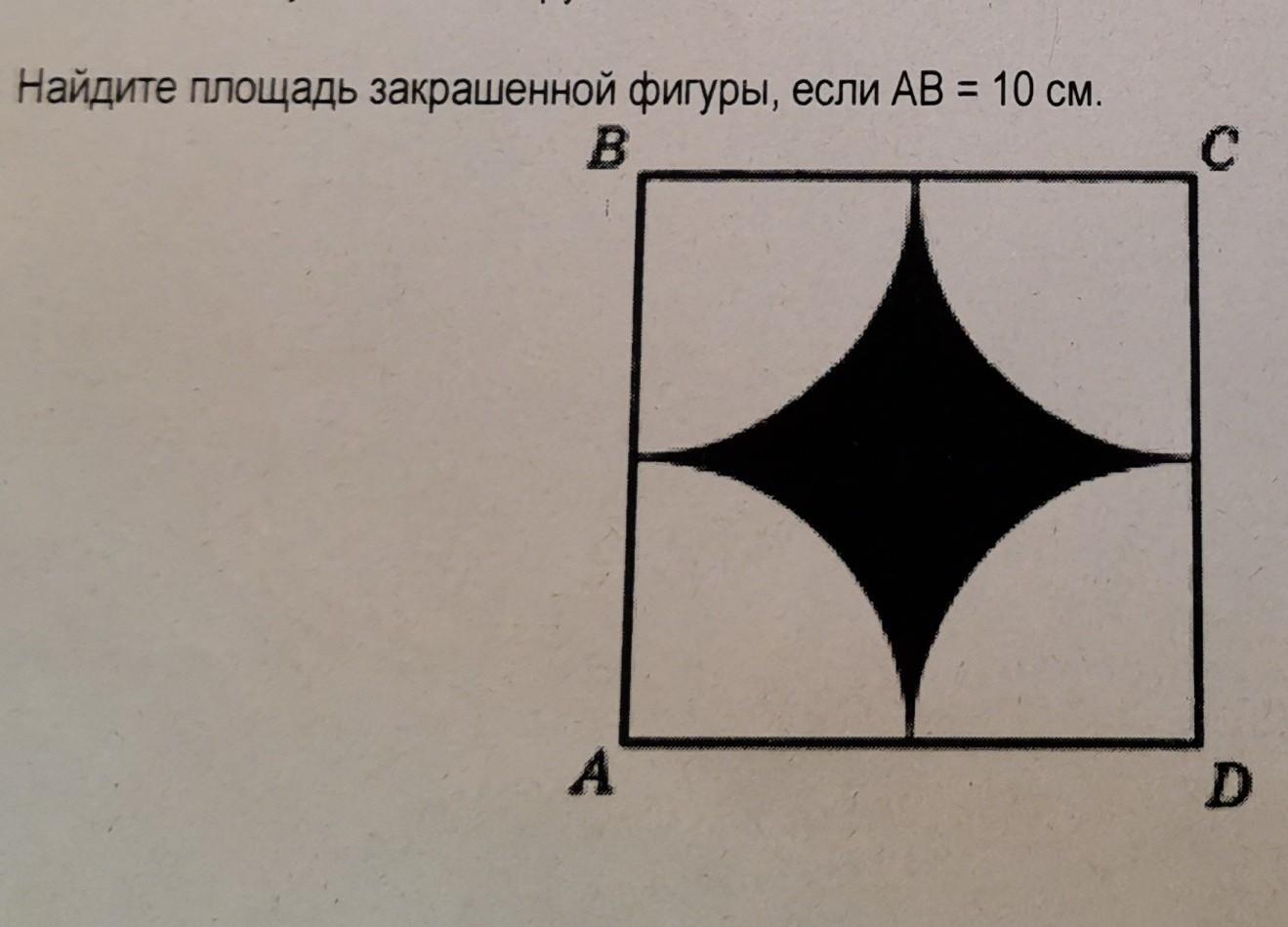
Найдите площадь закрашенной фигуры, если AB = 10 см.
Ответы
Ответ:
(100 - 25π) см²
Пошаговое объяснение:
Так как закрашенная фигура является симметричной относительно обеих осей, то это значит, что:
1) АВ = ВС = СD = AD = 10 см;
2) диагонали закрашенной фигуры пересекаются под углом 90°;
3) значит, ∠А = ∠В = ∠С = ∠D = 360° : 4 = 90°;
4) следовательно, вершины А, В, С и D являются центрами окружностей, из которых проведены радиусы:
АВ : 2 = ВС : 2 = CD : 2 = AD : 2 = 10 : 2 = 5 cм.
Следовательно, АВСD - квадрат, а все незакрашенные сегменты равны между собой, и каждый из них составляет 1/4 площади круга радиусом R = 5 см.
Значит, площадь закрашенной фигуры равна разности между площадью квадрата и сумме площадей четырёх одинаковых сегментов круга радиусом 5 см:
S = 10² - 4 · [(π·5²)/4] = (100 - 25π) см² ≈ 100-25·3,14 ≈ 100-78,5 ≈ 21,5 см²
Ответ: (100 - 25 π) см² ≈ 21,5 см²