Хоть кто-то знает ответ на этот вопрос? Помогите!
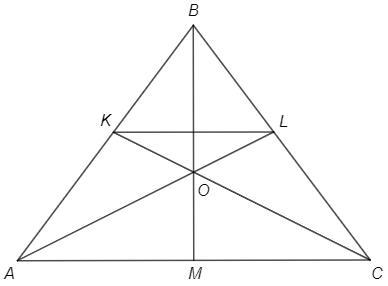
В равнобедренном треугольнике ABC боковая сторона АВ = 55, а высота, проведённая к основе АС - 44 см. Биссектриса AL & CK пересекаются в точке О. Найти площадь KOL
Ответы
В сантиметрах.
В равнобедренном треугольнике высота к основанию является также медианой и биссектрисой.
Как медиана BM делит основнание пополам, AC=2AM
По т Пифагора AM=33 (△ABM - египетский), AC=66
SABC=1/2 AC BM =12*11^2
Как биссектриса BM проходит через точку пересечения биcсектрис O.
Биссектриса делит сторону в отношении прилежащих сторон.
OM/BO =AM/AB =3/5 => OM/BM=3/8
Треугольники AOC и ABC имеют общее основание, следовательно их площади относятся как высоты.
SAOC/SABC =OM/BM =3/8
Биссектрисы треугольника делятся точкой пересечения в отношении суммы прилежащих сторон к противолежащей.
AO/OL =(55+66)/55 =11/5 =CO/OK
△AOC~△KOL (по двум пропорциональным сторонам и углу между ними)
Площади подобных фигур относятся как квадрат коэффициента подобия.
SAOC/SKOL =(11/5)^2
SKOL =(5/11)^2 *SAOC =(5/11)^2 *3/8 *SABC =112,5 (см^2)