Предмет: Геометрия, автор: safinvalentijn

ДАЮ 50 БАЛЛОВ ГЕОМЕТРИЯ 10 КЛАСС
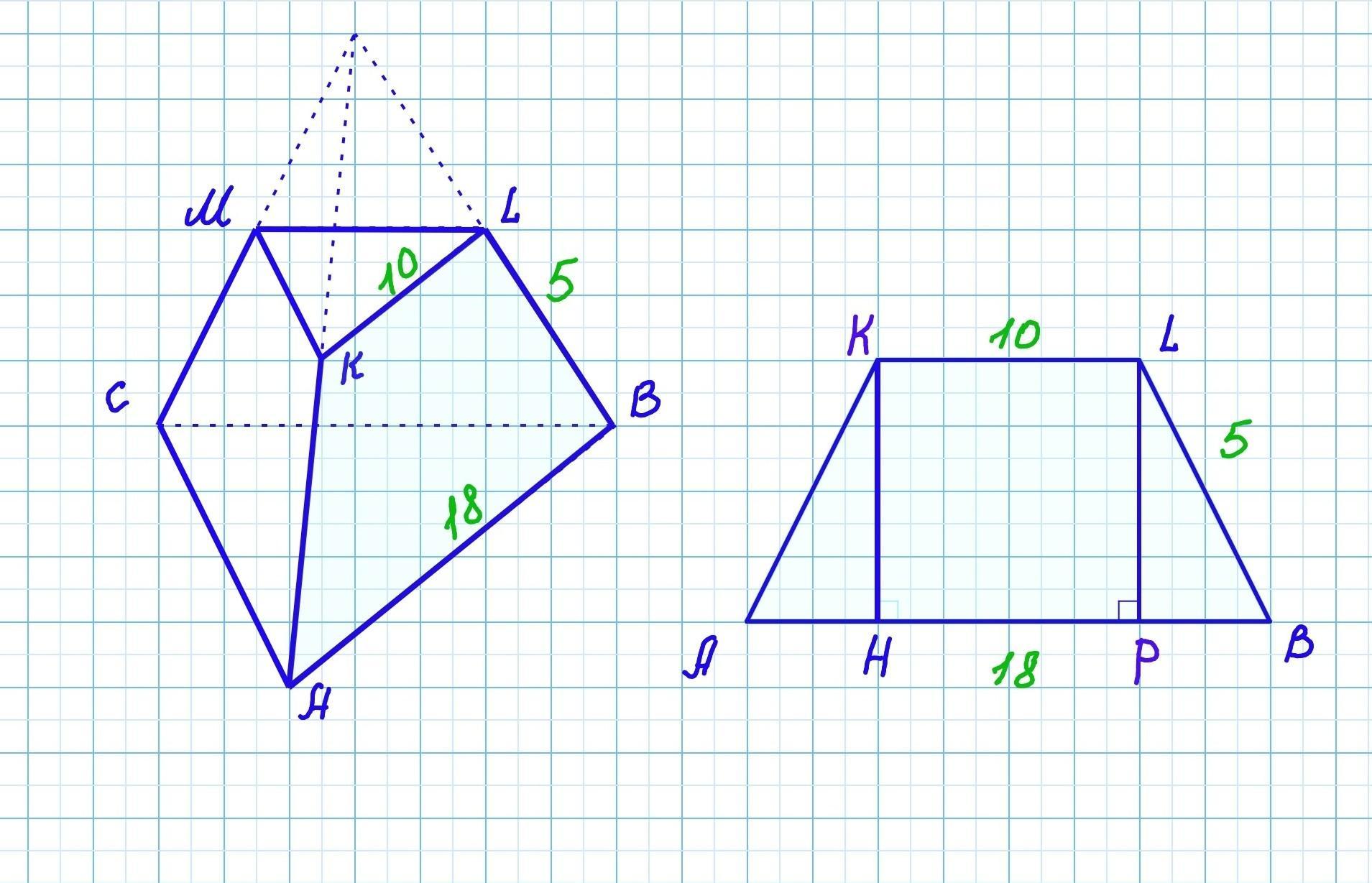
Найдите площадь боковой поверхности правильной треугольной усечённой пирамиды, стороны оснований которой равны 10 см и 18 см, а боковое ребро — 5 см.

Simba2017: это три одинаковые равнобедренные трапеции
Simba2017: высота каждой 3

Ответы

Автор ответа: ReMiDa
3

Ответ:

Площадь боковой поверхности правильной треугольной усеченной пирамиды равна 126 см²

Объяснение:

Боковая поверхность правильной треугольной усеченной пирамиды состоит из трёх равнобедренных трапеций ( т.к. основания усеченной пирамиды параллельны друг другу, а все боковые рёбра равны между собой)

  • Площадь трапеции равна полусумме её оснований умноженное на высоту.

S = \dfrac{a + b}{2} \times h

а = KL= 10 см, b = AB = 18 см, найдём высоту h.

Опустим перпендикуляры из вершины верхнего основания на нижнее. КН⟂АВ, LP⟂AB. Следовательно HKLP - прямоугольник. HP=KL=10 см, как стороны прямоугольника.

△АКН - прямоугольный (∠Н=90°), △BLP - прямоугольный (∠P=90°).

△AKH=△ BLP по гипотенузе и катету. (AK=LB - как рёбра правильной усеченной пирамиды; KH=LP - как высоты равнобедренной трапеции).

Следовательно АН=PB=(AB-KL):2=(18-10):2=4см

По теореме Пифагора найдём катет АН.

KH = \sqrt{ {AK}^{2} - {AH}^{2} } = \sqrt{ {5}^{2} - {4}^{2} } = \sqrt{ 25 - 16 } = \sqrt{9 } = 3 см

Площадь трапеции AKLB равна:

S = \dfrac{KL + AB}{2} \times KH = \dfrac{10 + 18}{2} \times 3 = 42 см²

Тогда площадь боковой поверхности правильной треугольной усеченной пирамиды равна:

Sб=3×S(AKLB)=3×42= 126 см²

#SPJ1

Приложения:
Предыдущий вопрос
Следующий вопрос
Похожие вопросы
Предмет: Окружающий мир, автор: Sheaanton
Краткое сообщение о Антарктиде
1 год назад
Предмет: Английский язык, автор: Indeika
Помогите составить портфолио What is life like for teenagers in your country? Collect information using the internet and write a short article for an English teenage magazine.Use pictures to illustrate your article.
Нужно слов 50
Пожалуйста, уважайте меня и себя. Все сообщения не по теме будут удаляться.
1 год назад
Предмет: Английский язык, автор: grabenkoira
1. The second witness's evidence more convincing. _it____ made me believe that the suspect is innocent..
a) are, it
b) is, it
c) are, they
d) is, they

2. In spring of following year we went____abroad and were absent several months. Навесні наступного року ми пішли за кордоном і були відсутній кілька місяців
a)__, the, ___
b) the, the, the
c) , ,
d) the, the

3. I see only five boys here. Where are ones?
a) another
b) others
c) the others
d) the other

4. You've been ____ working _____.
a) hardly, lately
b) hard, lately
c) hard, late
d) hardly, late

5. I ___ Jack lately. When ____ him last? — I ___ him two days ago. I ____ that he ____ very much.
a) did not see, have you seen, met, thought, changes
b) have not seen, did you see, met, think, changed
c) have not seen, you saw, met, think, changed
d) do not see, have you seen, have met, thought, would change

6. Noah Webster An American Dictionary of the English Language in two volumes in 1828, and since then it the recognized authority for usage in the United States.
a) published, became
b) has published, has become
c) published, was becoming
d) published, has become

7. I never them when I lived in London.
a) had met
b) have met

8. In case the weather ___ good, they ___ fishing
a) will be, will go
b) is, go
c) will be, go
d) is, will go

9. They ___ to build a new McDonalds in several days and ___ it by the end of the year.
a) will start, will finish
b) are starting, will have finished
c) start, will be finishing
d) start, are finishing

10. Сейчас здесь строится новый супермаркет.
a) is being built
b) is building
c) is built

11. The doctor there nothing to worry about if the fever ___ above 38,5°.
a) said, was, would not go
b) tells, is, will go
c) says, had been, went
d) said, was, did not go

12. There are a lot of people who expect your country ___ the same as their own.
a) not to be
b) not being
c) not be

13. The rain seems ___. Call the children in. I do not want them ___.
a) to be, to be got wet through
b) to be starting, to get wet through
c) to have started, to have got wet through
d) to have been started, to be getting wet through

14. I wonder if there is any use ___ ___ him.
a) trying, improving
b) trying, to improve
c) to try, to improve
d) to try, improving

15. She had a good practical knowledge of French __ as an interpreter for many years in France.
a) working
b) having worked
c) worked

16. She put down her book ___ me ___; and ___ me ___ took her workbasket and sat into one of the old-fashioned armchair.
a) to see, coming in, have welcomed, as usually
b) having seen, to come in, welcoming, usually
c) on seeing, come in, having welcomed, as usual
d) after seeing, having come in, to welcome, in a usual way

17. Mrs. Sparred ___ very beautiful when she was young. She has a fine face.
a) was to be
b) must have been
c) must be

18. You it long ago.
a) must do
b) should have done
c) needn't have done
d) are to do

19. Let's wait a little. He ___ .
a) may have come
b) could have come
c) may come
d) might have come

20. He had to earn ___ living at ___ an early age, ___?
a) ___, such, hadn’t he
b) his, such, didn’t he
c) himself, so, hadn’t he
d) to, so, didn’t he

21. 1 don't know how him. I wish I his name.
a) address, did not know
b) to address, knew
c) addressing, would know
d) to address, should know

22. ___ 1812 Russian fur traders established Fort Ross ___ California's northern coast and it functioned ___ a Russian trading post ___ 1841 when, ___ order from Alaska, the fort was dismantled.
a) in, on, as, until, by
b) on, at, as, by, through
c) at, in, like, till, at
d) during, along, like, in, by

23. He walked into ___ Green Park that he might cross to ___ Victoria Station and take ___ underground into ___City.
a) the, , the, the
b) the, the, the, the
c) ___ , ___, ___, ___
d) ___, ___, an, ___
1 год назад
Предмет: Математика, автор: dxaseleo26
Помогите и объясните пожалуйста
7 лет назад
Предмет: Математика, автор: Aleksa31tv
Помогите срочно, пожалуйста!
7 лет назад