Предмет: Алгебра,
автор: megumin228337
Помогите пожалуйста решить!
Приложения:
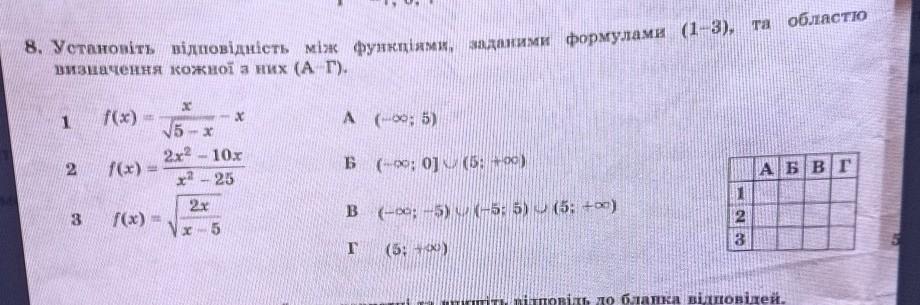
Ответы
Автор ответа:
1
Ответ: 1 - А , 2 - В , 3 - Б .
Знаменатель дроби не может быть равен 0 . Подкоренное выражение неотрицательно .
Б
megumin228337:
Спасибо
Похожие вопросы
Предмет: Русский язык,
автор: elkiigolkiYT
Предмет: Русский язык,
автор: маша10121
Предмет: Английский язык,
автор: maraok
Предмет: Математика,
автор: linavasilkina