Question

Окружность касается стороны треугольника в ее середине. Докажите что этот треугольник равнобедренный.​

Answer 1

Ответ:

Доказано, что треугольник АВС - равнобедренный.

Объяснение:

Вписанная  окружность касается одной из сторон треугольника в ее середине. Докажите что этот треугольник равнобедренный.

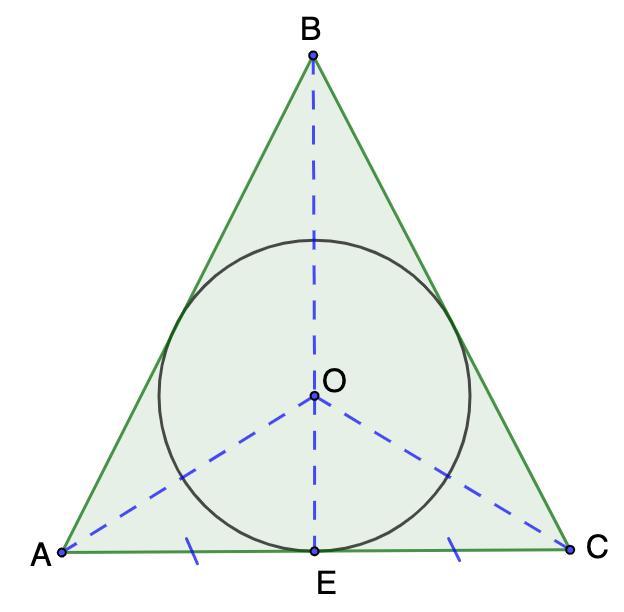
Дано: ΔАВС;

Окр.О - вписана в ΔАВС;

Е - точка касания;

АЕ = ЕС.

Доказать: ΔАВС - равнобедренный.

Доказательство:

1. Рассмотрим ΔАОС.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОЕ ⊥ АС ⇒ ОЕ - высота;

АЕ = ЕС (условие) ⇒ ОЕ - медиана.

• Если в треугольнике высота является медианой, то этот треугольник равнобедренный.

⇒ ΔАОС - равнобедренный.

АО = ОС

• В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой.

⇒ ∠АОЕ = ∠ЕОС.

2. Рассмотрим ΔАВО и ΔОВС.

АО = ОС (п.1)

ОВ - общая.

• Сумма смежных углов равна 180°.

⇒ ∠АОВ = 180° - ∠АОЕ

   ∠ВОС = 180° - ∠ЕОС

∠АОЕ = ∠ЕОС (п.1)

⇒ ∠АОВ =  ∠ВОС

ΔАВО = ΔОВС (по двум сторонам и углу между ними, 1 признак)

• В равных треугольниках против равных углов лежат равные стороны.

⇒ АВ = ВС

ΔАВС - равнобедренный.

#SPJ1