Question

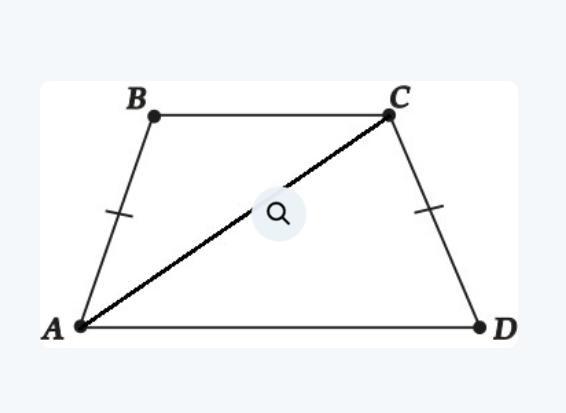
Равнобедренная трапеция ABCD основание AD =20 смПериметр равен 47 см.AC диагонали бисектрисса углаA.найти сторону трапеции

Answer 1

Вот решение:

∠BAC = ∠CAD т.к. AC - биссектриса.

∠BCA = ∠CAD т.к. данный углы накрест лежащие при параллельных прямых.

⇒ ∠BAC = ∠CAD ⇒ ΔABC - равнобедренный.

⇒ AB = BC = СD (AB = CD т.к. трапеция равнобедренная)

Пусть AB = BC = СD = x.

Тогда 3х + 20 = 47

3х = 27

х = 9

Ответ: AB = CD = 9