Question

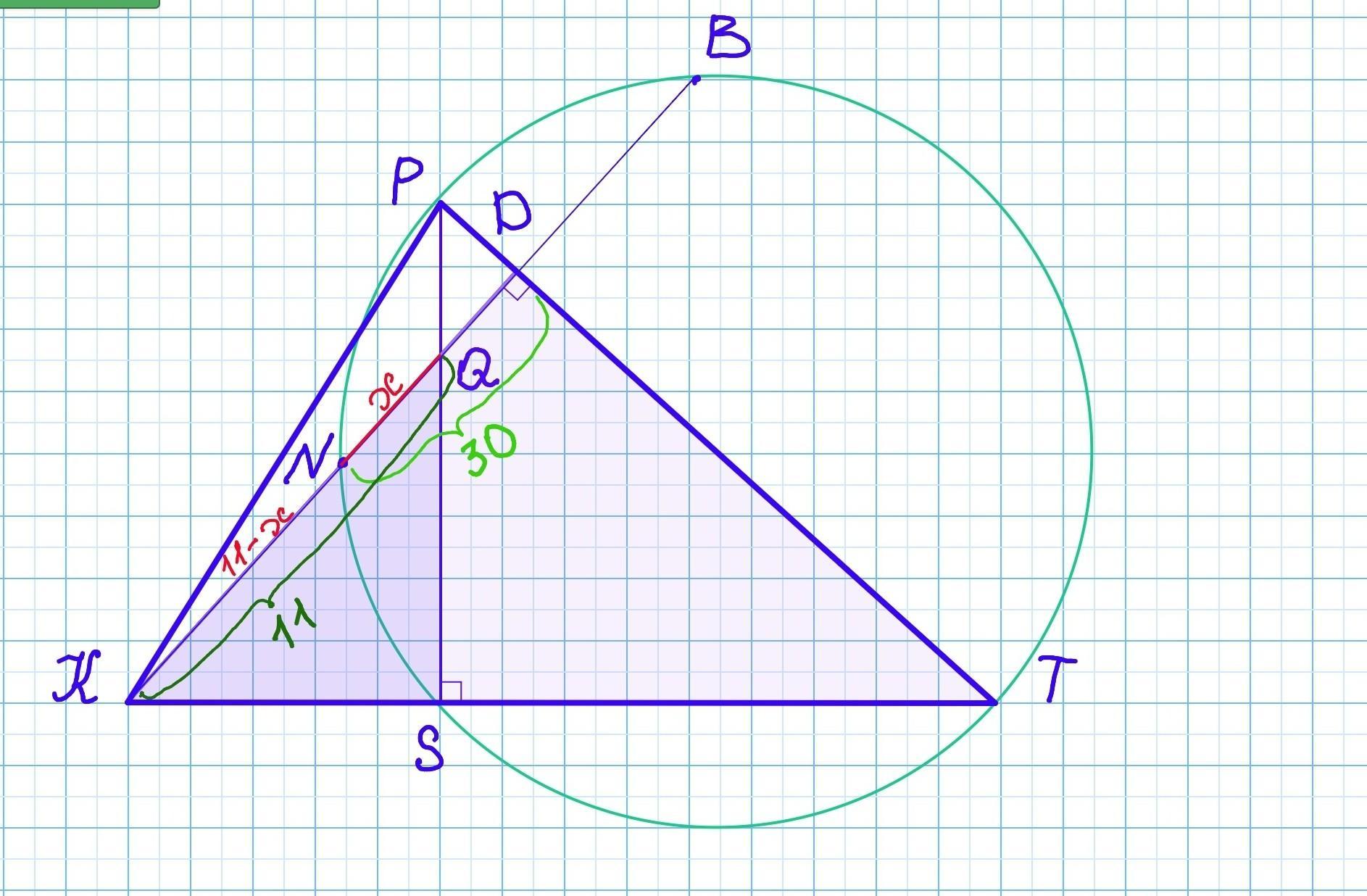
В произвольном остроугольном треугольнике КРТ высоты KD и PS пересекаются в точке Q. Через точки P, S, T проведена окружность, пересекающая KD в точке N, причём ND = 30, кQ = 11.
Найдите KD
найдите KN
Найдите NQ​

Answer 1

Ответ:

KD = 36 ед

KN = 6 ед

NQ = 5 ед

Объяснение:

Дан произвольный остроугольный △КРТ. Высоты KD и PS пересекаются в точке Q. KD⟂PT, PS⟂KT. Через точки P, S, T проведена окружность, пересекающая KD в точке N, причём ND = 30, KQ = 11.

Найдите KD

Hайдите KN

Найдите NQ

1) △KSQ подобен △KDT ( по двум углам ): ∠К - общий, ∠QSK=∠KDT=90°.

Из подобия треугольников следует пропорциональность соответственных сторон:

$\dfrac{KS}{KD} = \dfrac{KQ}{KT}$

( 1 ) KS • KT = KD • KQ

2) Продолжим отрезок KD до пересечения с окружностью. Получили точку В.

• Произведение отрезков секущих, проведенных из одной точки, равны.

( 2 ) KS • KT = KN • KB

3) Из ( 1 ) и ( 2 ) следует, что:

KD • KQ = KN • KB

4) Пусть NQ=х, тогда KN= 11-x.

KD = KN+ND = 11-x+30 = 41-x

KB = KN+ND+DB. ND=DB=30, т.к. диаметр, перпендикулярный хорде проходит через её середину. ( PT⟂NB ). Значит:

KB = 11-х+30+30 = 71-х

5) Решаем уравнение:

(41-х)•11 = (11-х)(71-х)

451-11х=781-71х-11х+х²

х²-71х+330=0

D=71²-4×330=3721=61²

$x_1= \frac{71+61}{2} =66$

- не подходит по смыслу,

$x_2= \frac{71-61}{2} = 5$

Таким образом:

NQ = 5 ед,

KN = 11-5 = 6 ед,

KD = 41-5 =36 ед.