Предмет: Геометрия,
автор: darky06
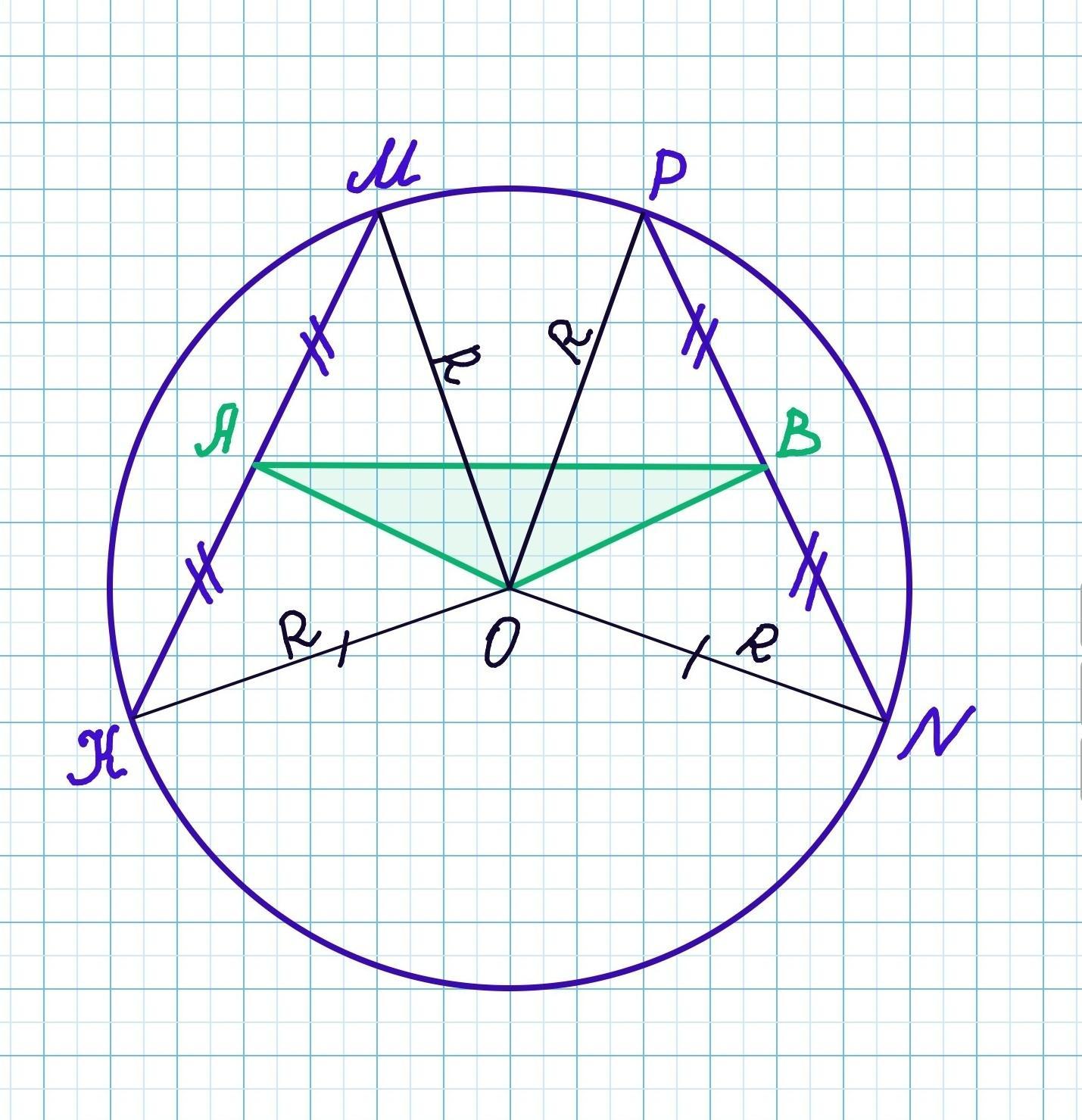
В окружности с центром О проведены две непараллельные хорды КМ и РN , причем КМ= РN. Точка А – середина КМ, точка В – середина Р N . Докажите, что треугольник АОВ равнобедренный.
СРОЧНО!
Ответы
Автор ответа:
8
Объяснение:
В окружности с центром О проведены две непараллельные хорды КМ и РN , причем КМ= РN. Точка А – середина КМ, точка В – середина РN . Докажите, что треугольник АОВ равнобедренный.
- Хорда — это отрезок, соединяющий две точки окружности.
Проведём радиусы ON, OP, OM и OK.
Рассмотрим треугольники OMK и OPN.
Так как ON=OK, OM=OP - как радиусы окружности, то они равнобедренные.
Точка А – середина КМ, точка В – середина РN, таким образом KA=AM=PB=BN.
Следовательно ОА - медиана △OMK, OB - медиана △OPN.
- Медиана в равнобедренном треугольнике является также высотой.
Поэтому треугольники OAM и OBP - прямоугольные.
У них:
AM=PB - по условию, OM=OP - как радиусы окружности.
△OAM=△OBP по гипотенузе и катету.
Из равенства треугольников следует равенство катетов: AO=OB.
- Треугольник в котором две стороны равны между собой по длине называется равнобедренным.
Таким образом мы доказали, что треугольник АОВ - является равнобедренным.
______
#SPJ1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: az18200184
Предмет: Русский язык,
автор: Nastik20042004
Предмет: Французский язык,
автор: kseniakustova
Предмет: История,
автор: gusi601
Предмет: Русский язык,
автор: pozimax99