Предмет: Алгебра,
автор: aliya9516
6. Упростите выражение:
Приложения:
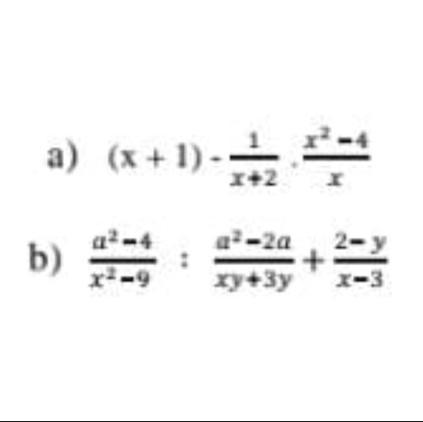
Ответы
Автор ответа:
1
Решение.
Воспользуемся формулой разности квадратов .
Похожие вопросы
Предмет: Окружающий мир,
автор: ирина1192
Предмет: Русский язык,
автор: теёмка1987
Предмет: Русский язык,
автор: Gulbanum1986mailru
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: Maloykinyru