Предмет: Алгебра,
автор: umikogaca92
П омогите пожалуйста срочно!!! Решите неравенство методом интервалов
Приложения:
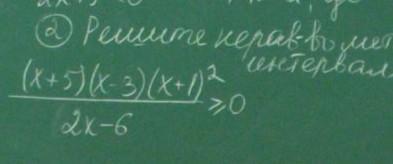
Ответы
Автор ответа:
1
Решение.
, ОДЗ:
.
Числитель обращается в 0 при х= -5 , х= -1 .
На числовой оси отметим точки -5 , -1 и 3 . Подсчитаем знаки функции в полученных промежутках: - - - - - [-5 ] + + + + + [-1 ] + + + + (3) + + + + +
Ответ:
Приложения:

umikogaca92:
А можешь точнее показать на листке, отрезок этот
вставила картинку
Похожие вопросы
Предмет: Английский язык,
автор: пранголлгнеагкнла122
Предмет: Английский язык,
автор: eatoty
Предмет: Русский язык,
автор: milaplotnikova
Предмет: История,
автор: andrejnmchenko
Предмет: Русский язык,
автор: z12316