Предмет: Алгебра,
автор: sonechko6006
9cos2x-4cos^2x=11sin2x+9
помогите решить ,10 класс алгебра
Приложения:
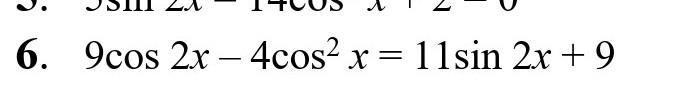
Ответы
Автор ответа:
1
Ответ:
Заменим tan(x)=t
D=121-72=49
Похожие вопросы
Предмет: Русский язык,
автор: CarlosFrederick
Предмет: Английский язык,
автор: Банан1511
Предмет: Русский язык,
автор: maryse9788
Предмет: Математика,
автор: rostik123123123654
Предмет: Русский язык,
автор: pds270109