Question

Тригонометрические функции угла и числового аргумента. Графики тригонометрических функций
Помогите пожалуйста
Очень срочно
спасибо заранее.​

Answer 1

Ответ:

Г, А

Пошаговое объяснение:

Вспомним определения

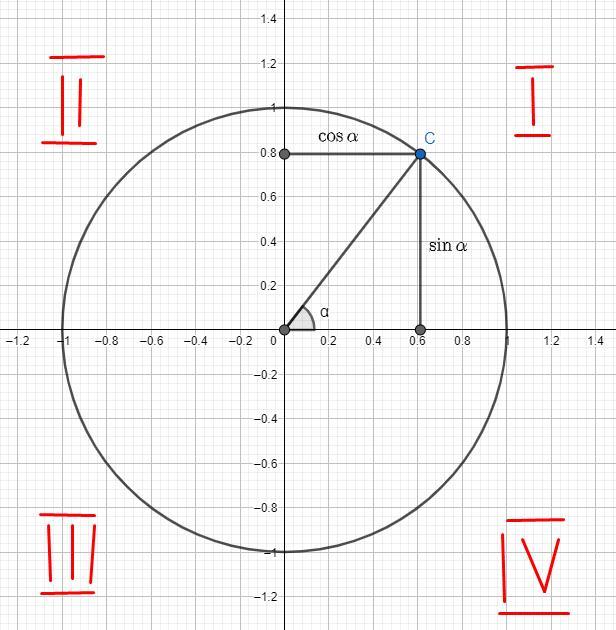
1. $\sin \alpha$ - синус, в прямоугольном треугольнике отношение катета, противолежащего углу $\alpha$ к гипотенузе. Выражается ординатой ($y$) точки на еденичной окружности.

$-1\leq \sin\alpha\leq 1$ для любого угла $\alpha$

Синус положителен в $\mathrm{I}$ и $\mathrm{II}$ четвертях, и отрицателен в $\mathrm{III}$ и $\mathrm{IV}$ (см. рис)

2. $\cos \alpha$ - косинус, в прямоугольном треугольнике отношение катета, прилежащего к углу $\alpha$ у гипотенузе. Выражается абсциссой ($x$) точки на еденичной окружности.

$-1\leq \cos \alpha\leq 1$ для любого угла $\alpha$

Косинус положителен в $\mathrm{I}$ и $\mathrm{IV}$ четвертях, отрицателен в $\mathrm{II}$ и $\mathrm{III}$ (см. рис)

3. $\mathrm{tg}\,\alpha$ - тангенс, в прямоугольном треугольнике отношение катета, противолежащего углу $\alpha$ к прилежащему (отношение синуса и косинуса)

$\mathrm{tg}\,\alpha=\dfrac{\sin\alpha}{\cos\alpha}$

4. $\mathrm{ctg}\,\alpha$ - котангенс, в прямоугольном треугольнике отношение катета, прилежащего к углу $\alpha$ к противолежащему (отношение косинуса и синуса)

$\mathrm{ctg}\,\alpha=\dfrac{\cos\alpha}{\sin\alpha}$

5. Важная оговорка про углы и про четверти.

Углы $0^\circ\leq \alpha\leq 90^\circ$ находятся в $\mathrm{I}$ четверти
Углы $90^\circ\leq \alpha\leq 180^\circ$ находятся во $\mathrm{II}$ четверти
Углы $180^\circ\leq \alpha\leq 270^\circ$ находятся в $\mathrm{III}$ четверти
Углы $270^\circ\leq \alpha\leq 360^\circ$ находятся в $\mathrm{IV}$ четверти

Укажите верное неравенство

A) $\sin 110^\circ < 0$

Угол в $110^\circ$ находится во $\mathrm{II}$ четверти (тупой угол). Его синус положительный, т.е. неравенство неверное

Б) $\cos 210^\circ > 0$

Угол $210^\circ$ находится в $\mathrm{III}$ четверти. Его косинус отрицателен, т.е. неравенство неверное

B) $\mathrm{tg}\,155^\circ > 0$

Для тангенса посмотрим на знаки синуса и косинуса.

Угол $155^\circ$ находится в $\mathrm{II}$ четверти. Его синус положителен, а косинус отрицателен, их частное отрицательно, т.е. неравенство неверное

Г) $\mathrm{ctg}\,225^\circ > 0$

Для котангенса так же посмотрим на знаки косинуса и синуса

Угол $225^\circ$ лежит в $\mathrm{III}$ четверти, И синус и косинус отрицательны, тогда их отношение положительно, т.е. неравенство верное

Д)  $\mathrm{ctg}\,115^\circ\cdot\mathrm{tg}\,115^\circ < 0$

Тангенс и котангенс одного угла взаимообратные, и их произведение 1, что больше 0. Неравенство неверное

Множеством решений какого неравенства является множество действительных чисел?

В этом задании необходимо вспомнить, что $-1\leq \sin\alpha\leq 1$ и $-1\leq \cos \alpha\leq 1$ для любого угла $\alpha$.

Если в неравенстве получается, что при любых значениях $\alpha$ выполняются неравенства выше, то множество решений  исходного неравенства - любое число или множество действительных чисел.

A) $\cos x > -2$

Косинус всегда больше $-2$ при любых значениях $x$. Решение - множество действительных чисел

Б) $\cos x < 1$

Косинус может принимать значение $1$ (при угле $0^\circ$, $360^\circ$, ...), Поэтому решением не является множество всех действительных чисел

B) $\cos x > 1$

Косинус всегда не больше 1. Неравенство не имеет решений.

Г) $\cos x > -1$

Косинус может быть равен $-1$, например, при угле в $180^\circ$, поэтому решением не является множество всех действительных чисел

Д) $\cos x > 2$. Косинус всегда не больше 1. А 2 он и подавно не больше. Так что решений нет.