Question

В прямоугольном треугольнике гипотенуза равна 10 см, один из катеров равна 8 см. Найдите другой катет этого треугольнике

Answer 1

Ответ:

6 см

Формулы:

Теорема Пифагора

Она гласит: "В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы".

То есть, $a^{2} + b^{2} = c^{2}$,

где $a$ - первый катет, $b$ - второй катет, $c$ - гипотенуза.

Итак, проверим.

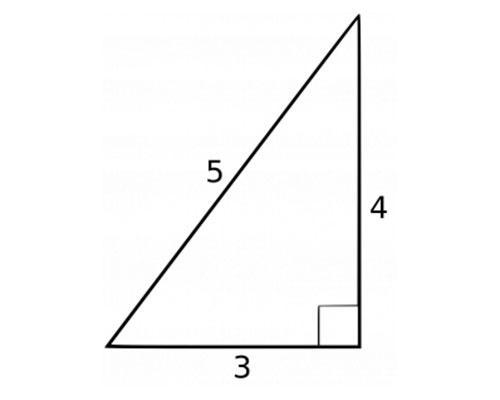
Треугольник реугольник со сторонами 3, 4, 5 (запомните эти числа) - см. приложенный рис.1. Проверим формулу Пифагора:

$3^{2} + 4^{2} = 5^{2}\\9 + 16 = 25$

На самом деле работает.

Пифагорова Троица

Пифагорова тройка — это тройка, в которой a и b не имеют общих простых делителей и являются сторонами прямоугольного треугольника:

• 3 4 5 | 9+16=25
• 5 12 13 | 25+144=169
• 7 24 25 | 49+576=625
• 8 15 17 | 64+225=289
• 9 40 41 | 81+1600=1681
• 11 60 61 | 121+3600=3721
• 12 35 37 | 144+1225=1369
• 13 84 85 | 169+7056=7225

Пошаговое объяснение:

$a^{2} + b^{2} = c^{2}$

$x^{2} + 8^{2} = 10^{2}\\x = \sqrt{10^{2}-8^{2}} \\x = \sqrt{100-64}\\x = \sqrt{36}\\x = 6$