Question

Розв'язати систему рівнянь з двома змінними трьома способами (графічний, додавання, підстановки)
будь ласкааа​

Answer 1

Объяснение:

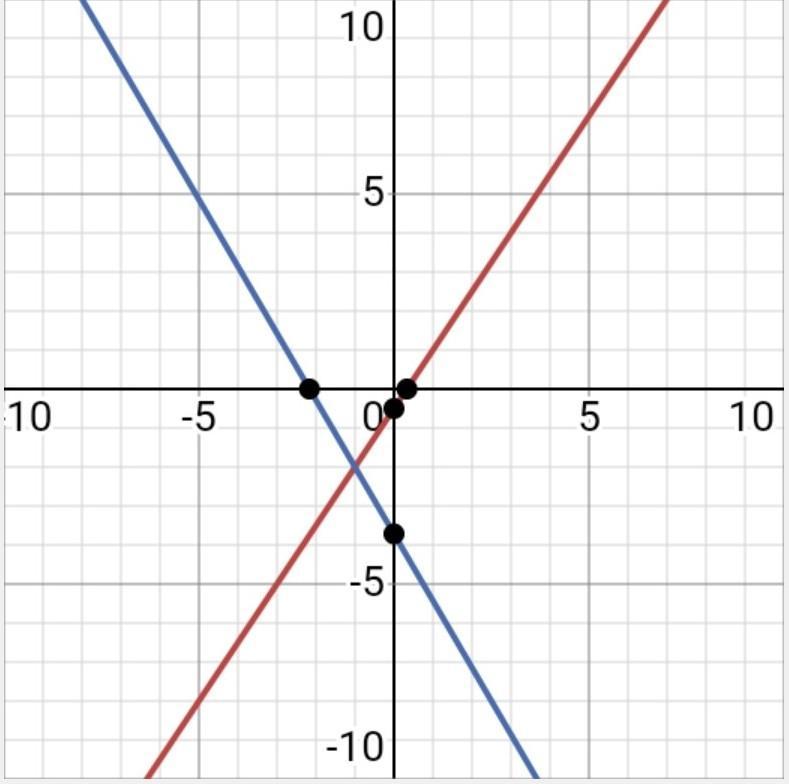
Графический способ :

{3х-2у=1

{12х+7у= - 26

3х-2у=1 красная

-2у=1-3х

У= 3/2х-1/2

Х 0 1/3

У - 1/2 0

12х+7у= - 26 синяя

7у= - 26-12х

У= - 12/7х-26/7

Х 0 13/6

У - 26/7 0

Решение точка пересечения (-1;-2)

2 сложения

{3х-2у=1 |×(-4)

{12х+7у= - 26

{-12х+8у= - 4

{12х+7у= - 26

+ —————

15у= - 30

У= - 2

3х=1+2у

3х=1+2×(-2)

3х=1-4

3х = - 3

Х= - 1

Ответ : (-1;-2)

3 подстановки

{3х-2у=1 => 3х=1+2у => х=1/3+2/3у

{12х+7у= - 26

12(1/3+2/3у)+7у= - 26

4+8у+7у= - 26

15у= - 26-4

15у= - 30

У= - 2

Х= 1/3+2/3×(-2)

Х=1/3-4/3

Х= - 1

Ответ : (-1;-2)

Answer 2

Ответ:

(x;y) = (-1;-2)

Объяснение:

$\displaystyle \left \{ {{3x-2y=1} \atop {12x+7y=-26}} \right.$

1) Сложение

$\displaystyle \left \{ {{3x-2y=1|*(-4)} \atop {12x+7y=-26}} \right. < = > +\left \{ {{-12x+8y=-4} \atop {12x+7y=-26}} \right. < = > 15y=-30|:15 < = > y=-2$
Подставим полученное значение в одно из уравнений
$\displaystyle 3x-2*(-2) = 1;$
$\displaystyle 3x+4 = 1;$
$\displaystyle 3x = 1-4;$
$\displaystyle 3x = -3|:3;$
$\displaystyle x=-1$

2) Подстановка

$\displaystyle \left \{ {{3x-2y=1} \atop {12x+7y=-26}} \right. < = > \left \{ {{x=\frac{1+2y}{3} } \atop {12x+7y=-26}} \right. < = > \left \{ {{x=\frac{1+2y}{3} } \atop {12*\frac{1+2y}{3} +7y=-26}} \right. < = > \left \{ {{x=\frac{1+2y}{3} } \atop {4*(1+2y)+7y=-26}}$
Рассмотрим отдельно 2-ое уравнение системы
$\displaystyle 4*(1+2y)+7y=-26;$
$\displaystyle 4+8y+7y=-26;$
Перенесём все неизвестные влево, а известные вправо
$\displaystyle$$\displaystyle 15y=-26-4;$
$\displaystyle 15y=-30|:15;$
$y=-2$
Подставим полученное значение в х
$\displaystyle x=\frac{1+2*(-2)}{3} < = > x=\frac{1-4}{3} < = > x=\frac{-3}{3} < = > x=-1$

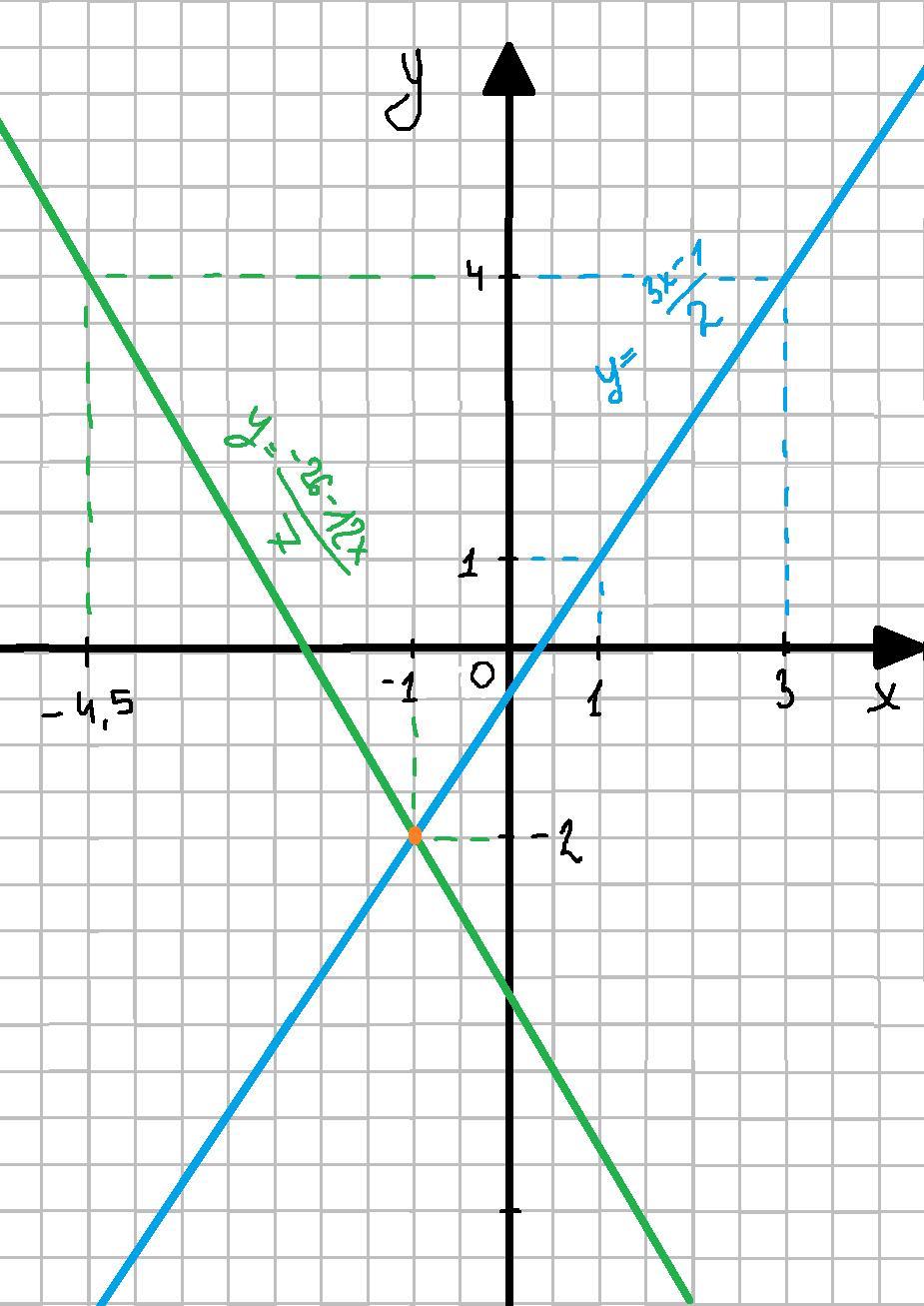
3) Графический

$\displaystyle \left \{ {{3x-2y=1} \atop {12x+7y=-26}} \right. < = > \left \{ {{y=\frac{3x-1}{2} } \atop {y=\frac{-26-12x}{7} }} \right.$
Найдём точки для каждой прямой
y₁(1) = (3*1-1)/2 = (3-1)/2 = 2/2 = 1
y₁(3) = (3*3-1)/2 = (9-1)/2 = 8/2 = 4
y₂(-1) = (-26-12*(-1))/7 = (-26+12)/7 = -14/7 = -2
y₂(4,5) = (-26-12*(-4,5))/7 = (-26+54)/7 = 28/7 = 4

Построим обе прямые (см. вложение)

Видно, что прямые пересекаются в точке (-1;-2), что и является решением