Предмет: Алгебра,
автор: ulianapaziuchenko
будь ласочка срочно!!!
Приложения:
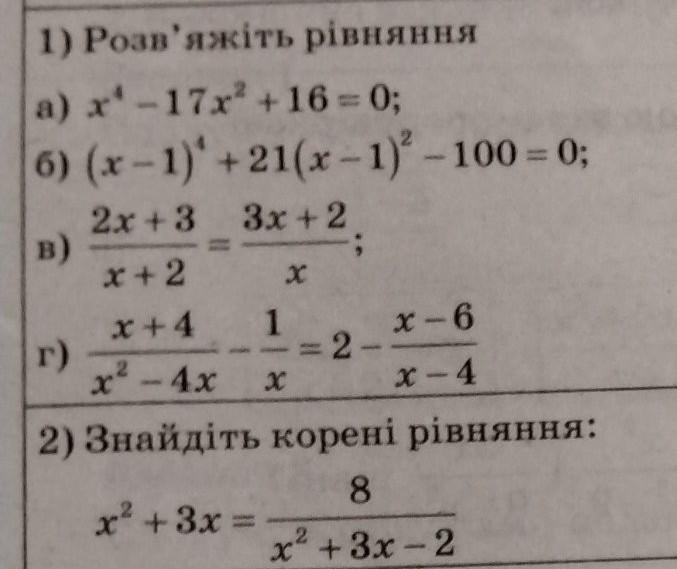
Ответы
Автор ответа:
0
Объяснение:
1)
Пусть х²=t≥0 ⇒
Ответ: x₁=-1, x₂=1, x₃=-4, x₄=4.
Пусть (х-1)²=t≥0 ⇒
Ответ: x₁=-1, x₂=3.
ОДЗ: х+2≠0 х≠-2 х≠0.
Ответ: x₁=-4, x₂=-1.
ОДЗ: х-4≠0 х≠4 х≠0.
Ответ: x=-2.
2)
Пусть х²+3х=t ⇒
Ответ: x₁=-2, x₂=-1, x₃=-4, x₄=1.
Похожие вопросы
Предмет: Русский язык,
автор: лера1431
Предмет: Русский язык,
автор: ДядяВасяПетросян
Предмет: Английский язык,
автор: tomilina1989
Предмет: Русский язык,
автор: mamedzade2014
Предмет: Физика,
автор: VatikanikLusik33