Предмет: Алгебра,
автор: kvize91
срочно самостояткльная робота пж
Приложения:
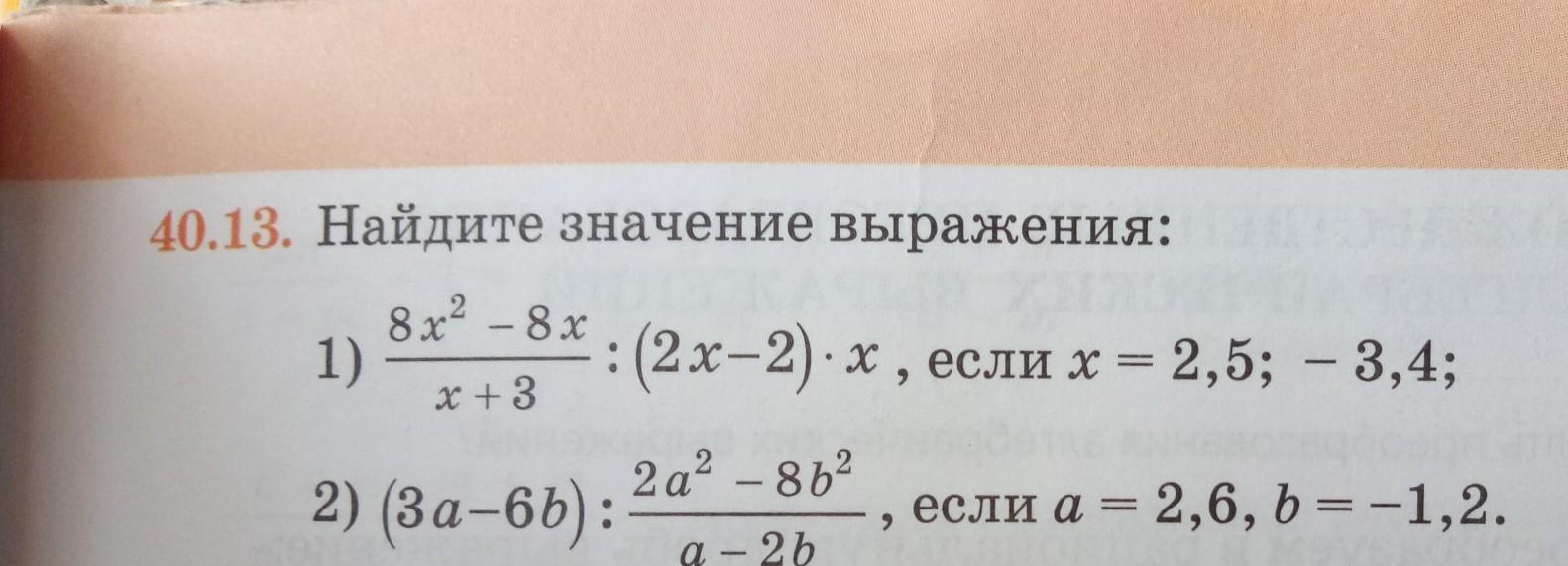
Ответы
Автор ответа:
0
Решение.
Найдём значение\я этого выражения при х=2,5 и х=-3,4 .
Найдём значения этого выражения при a=2,6 и b= -1,2 .
Похожие вопросы
Предмет: Русский язык,
автор: fairfly
Предмет: Русский язык,
автор: ладыженской
Предмет: Русский язык,
автор: Catalinawow
Предмет: История,
автор: AdamLee