Предмет: Алгебра,
автор: Dila5464
решите неравенства решите неравенство
Приложения:
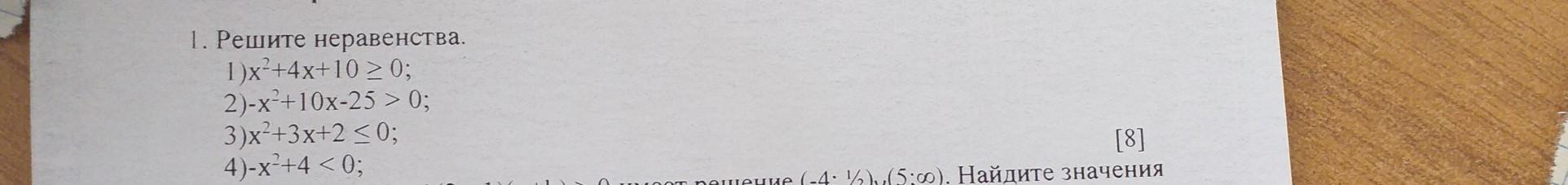
Ответы
Автор ответа:
0
Решение.
Выделим полный квадрат:
Если к квадрату какого-либо выражения, который принимает только неотрицательные значения, прибавить положительное число 6, то получим положительное значение суммы при любых значениях переменной х .
Решений нет, так как квадрат любого выражения не может принимать отрицательные значения.
Применяем формулу разности квадратов.
Метод интервалов . Нули функции х= -1 , х= -2 .
Знаки: + + + + + [-2 ] - - - [-1 ] + + + + +
Знаки: + + + + + (-2) - - - (2) + + + + +
Похожие вопросы
Предмет: Русский язык,
автор: Знания565
Предмет: Другие предметы,
автор: 354560
Предмет: Окружающий мир,
автор: ДанькаЛОЛолошка
Предмет: Алгебра,
автор: abgustina
Предмет: Химия,
автор: kate7799