Предмет: Математика,
автор: Аноним
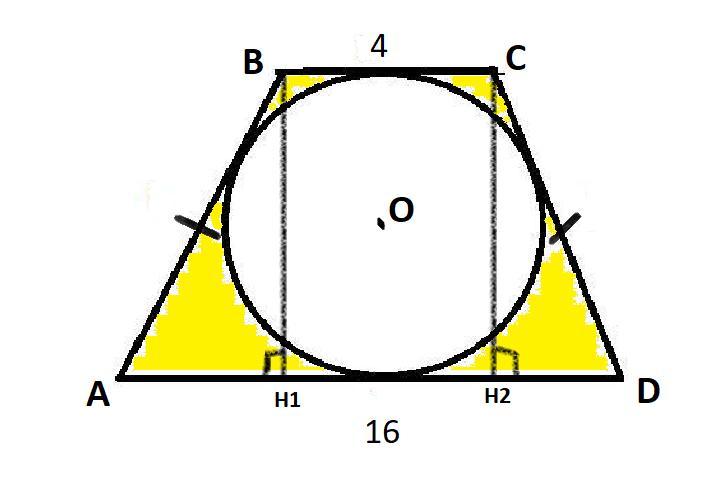
Стороны равнобедренной трапеции касаются окружности с центром в точке О. Основания трапеции равны 4 см и 16 см. Из трапеции случайным образом выбирается точка. Найдите вероятность того, что она не принадлежит кругу, ограниченному данной окружностью.
Ответы
Автор ответа:
24
Ответ:
вероятность того, что точка не принадлежит кругу, ограниченному данной окружностью, равна 1 - π / 5.
Пошаговое объяснение:
Дано:
ABCD - трапеция
AB = CD
BC = 4
AD = 16
вписанная в трапецию окружность (центр в т. О)
Найти: вер-ть, что случайным образом выбранная из трапеции точка находится вне окружности.
Решение:
• Чтобы найти искомую вероятность, надо площадь, куда должна попасть точка (желтого цвета на чертеже), разделить на площадь трапеции.
• Найдем эти площади:
(I) Площадь трапеции
- Если окружность вписана в равнобедренную трапецию, то ее средняя линия равна ее боковой стороне.
- Средняя линия: (BC + AD) / 2 = (4 + 16) / 2 = 10.
- => AB = CD = 10.
- Опустим два перпендикуляра BH1 и ВН2 на нижнее основание.
- Тогда Н1BCH2 - прямоугольник, поэтому Н1Н2 = ВС = 4.
- Т.к. трапеция равнобокая, АН1 = Н2D = (AD - H1H2) / 2 = (16 - 4) / 2 = 6.
- Рассмотрим треугольник АВН1: прямоугольный, АВ = 10, АН1 = 6 => BH1 = 8 (пифагорова тройка).
- ВН1 - высота (по построению).
- S(ABCD) = ((BC + AD) / 2) * BH1 = 10 * 8 = 80.
(II) Площадь желтой области
- Эту площадь можно найти, если вычесть площадь круга из площади трапеции.
- Если в трапецию вписана окружность, то ее диаметр будет равен высоте трапеции.
- => d = BH1 = 8.
- => r = d / 2 = 4.
- Площадь круга равна: S(кр.) = π*
= 4*4*π = 16π.
- Тогда площадь искомой области равна: S(обл.) = S(ABCD) - S(кр.) = 80 - 16π.
• Найдем вероятность:
p = S(обл.) / S(ABCD) = (80 - 16π) / 80 = 1 - π / 5.
Итого, ответ: 1 - π / 5.
#SPJ1
Приложения:
allyaaswrr:
НИХЕРАААААЯ НЕ ПОНЯТНГ
Правильно??
Похожие вопросы
Предмет: Окружающий мир,
автор: ДанькаЛОЛолошка
Предмет: Русский язык,
автор: абл5
Предмет: Русский язык,
автор: oksana20034
Предмет: Русский язык,
автор: Kostik8682