Предмет: Математика,
автор: ТвойНочнойКошмар
Даю 100 баллов! Помогите решить интеграл (полное решение). Ответы не по теме – в бан!
Приложения:
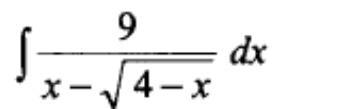
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:
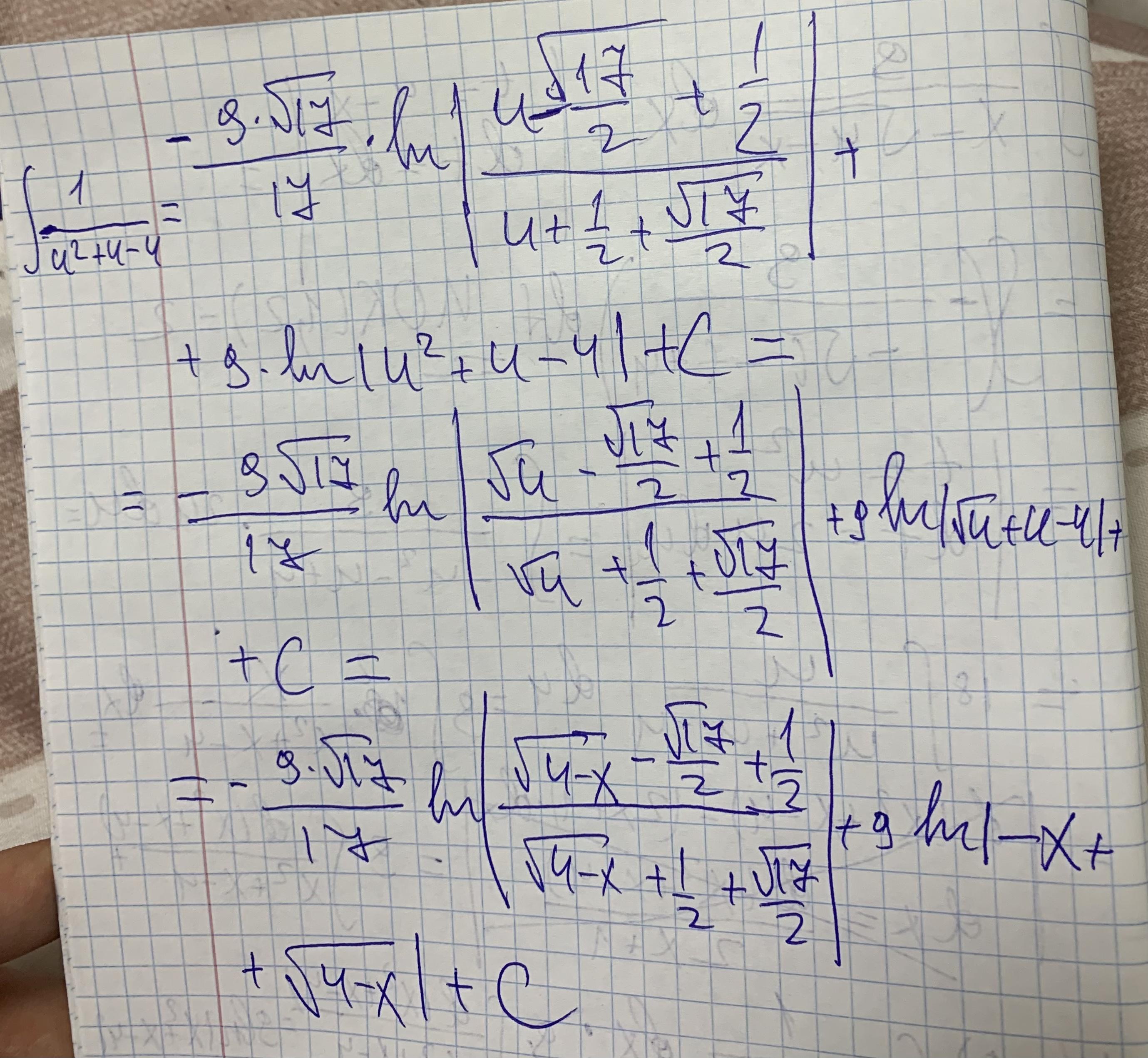
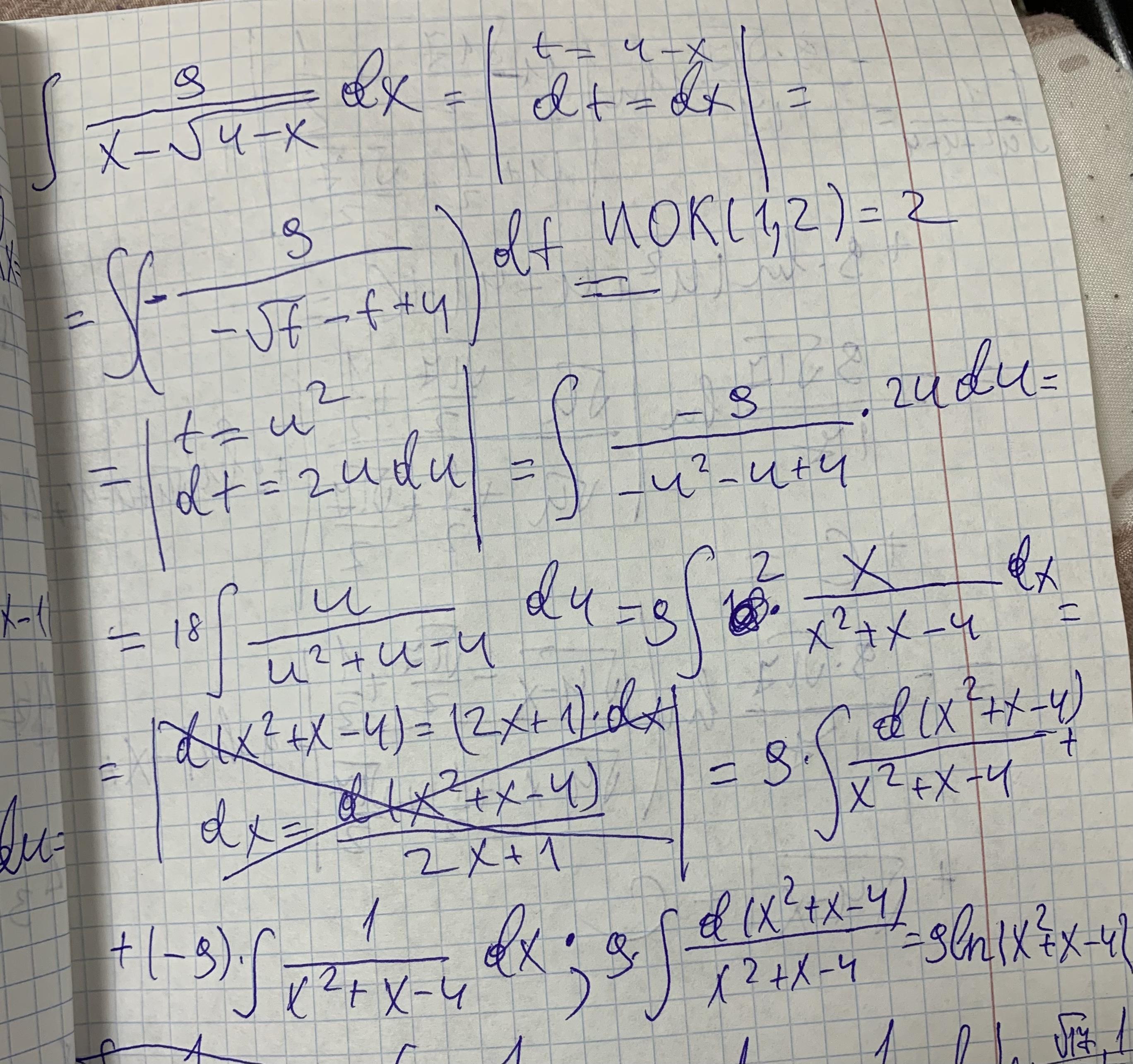
akameshev100:
Вроде правильно.
Спасибо огромное в очередной раз :) не совсем уловила, кто из вас раньше ответил
Автор ответа:
1
Вычисления:
isamars, можешь помочь с заданием?
Спасибо огромнейшее) Не уловила, кто из вас раньше ответил!!!
один раз при выборе вы дали корону ему. теперь моя очередь)
Ок) думаю, справедливо :)
Похожие вопросы
Предмет: Русский язык,
автор: ElizaDevil1
Предмет: Окружающий мир,
автор: КарнаSim
Предмет: Английский язык,
автор: Olivia179
Предмет: Русский язык,
автор: Alina6483
Предмет: Математика,
автор: kiki6622