Question

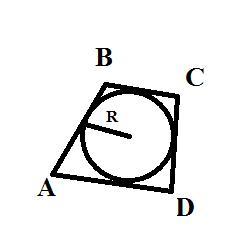
В трапеции вписан круг радиусом 4 см. Боковые стороны трапеции равны 12 см и 10 см. Найдите площадь трапеции

Українською:
У трапеції вписане коло радіусом 4 см.Бічні сторони трапеції дорівнюють 12 см і 10 см.Знайдіть площу трапеції


Нужно именно с решением. Заранее приношу свою благодарность за помощь

Answer 1

Дано:

R = 4 см

AB = 12 см (см. рис.)

DC = 10 см (см. рис.)

Найти:

S

Решение:

1. Если окружность вписана в трапецию, то AB + CD = BC + AD (свойство трапеции, в которую вписана окружность). И наоборот, если AB + CD = BC + AD, то в трапецию можно вписать окружность.

2. Площадь трапеции равна полусумме оснований умноженной на высоту, т.е.:

$S = \frac{BC + AD}{2} * h$

3. Радиус окружности, вписанной в трапецию равен половине высоте трапеции:

$R = \frac{h}{2}$

Вот эти 3 пункта нужно знать для решения этой задачи. Итак, сначала найдём высоту трапеции:

h = 2 * R = 2 * 4 = 8 (см)

Теперь воспользуемся первым свойством и найдём сумму оснований:

BC + AD = AB + CD = 12 + 10 = 22 (см)

Теперь найдём площадь:

$S = \frac{22}{2} * 8 = 11 * 8 = 88$ (см²)

Ответ: S = 88 см²