Предмет: Алгебра,
автор: Reideen
Решить с использованием двойного интеграла
Приложения:
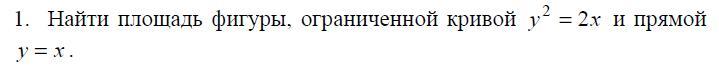
Ответы
Автор ответа:
2
Ответ:
квадратных единиц
Примечание:
Для вычисления двойного интеграла сведем его к повторному интегралу. Будем интегрировать по y, поэтому приведения в общем
виде к повторному интегралу двойного по области будет в виде:
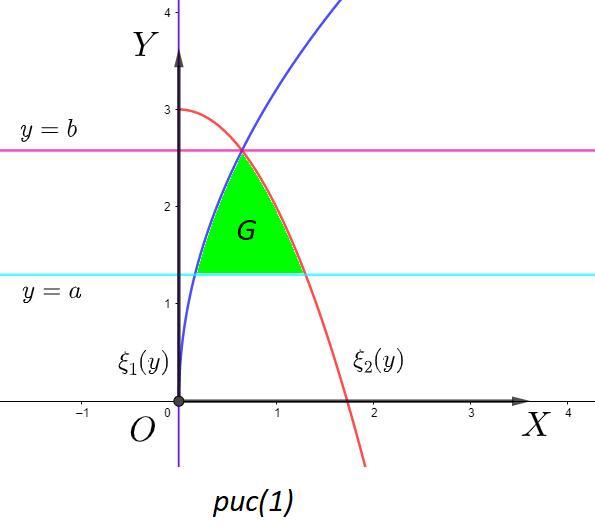
При этом функции - функции ограничивающие область слева и справа соответственно (смотрите рис(1)).
Объяснение:
По теореме площадь ограниченной области плоскости:
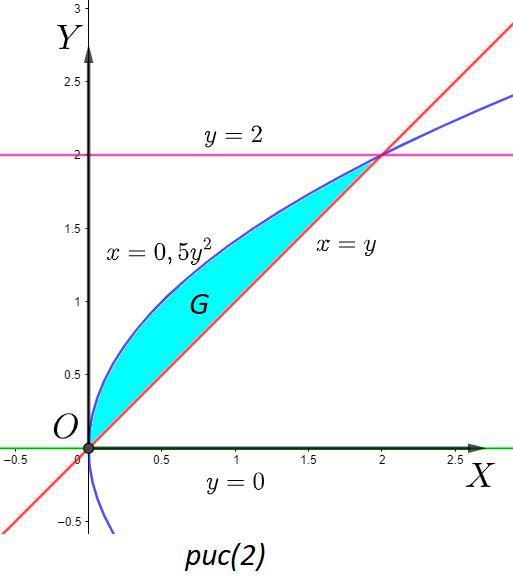
Смотрите рис(2)
Область
Найдем ординату пересечения графиков и
или
или
Границы интегрирования: от 0 до 2
квадратных единиц.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: кира508
Предмет: Английский язык,
автор: Мурка2006
Предмет: Другие предметы,
автор: кот582
Предмет: Українська мова,
автор: yli123568970
Предмет: Химия,
автор: andronovichveniamin5