Question

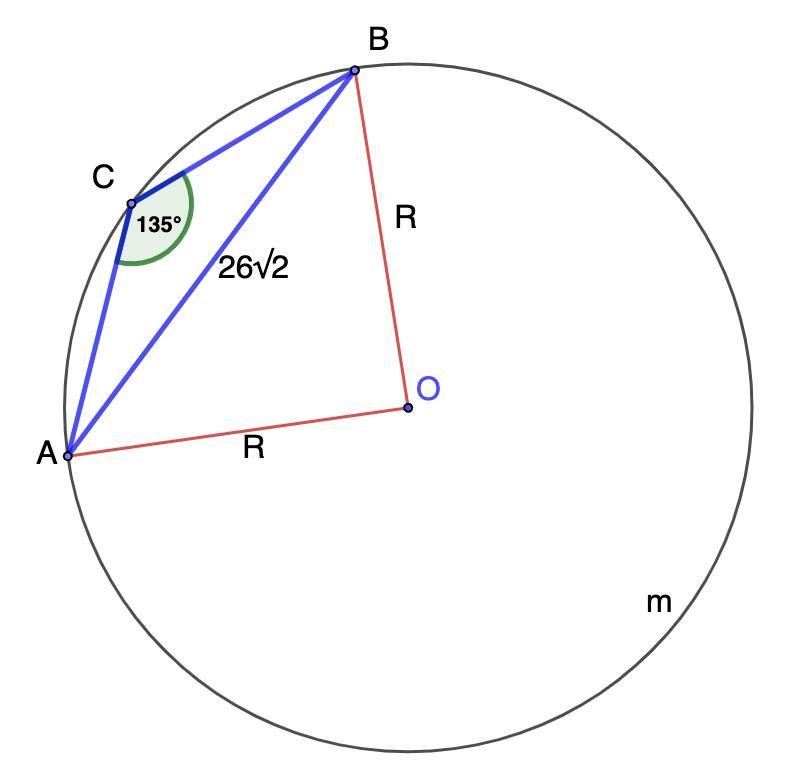
В треугольнике ABC угол C 135°, AB=26√2. Найдите радиус окружности, описанной около треугольника.
​

Answer 1

Ответ:

Радиус окружности, описанной около треугольника равен 26 ед.

Объяснение:

В треугольнике ABC угол C 135°, AB=26√2. Найдите радиус окружности, описанной около треугольника.

1 Способ.

Дано: ΔАВС;

Окр.О,R - описана около ΔАВС;

∠С = 135°;

АВ = 26√2.

Найти: R.

Решение:

∠С = 135° - вписанный.

• Вписанный угол равен половине градусной меры дуги, на которую он опирается.

⇒ ◡AmB = 135° · 2 = 270°

• Градусная мера окружности равна 360°.

⇒ ◡АСВ = 360° - ◡AmB = 360° - 270° = 90°

• Центральный угол равен градусной мере дуги, на которую он опирается.

⇒ ∠АОВ = 90° (центральный)

Рассмотрим ΔАОВ - прямоугольный.

АО = ОВ = R

⇒ ΔАОВ  - равнобедренный.

По теореме Пифагора:

AO² + OB² = AB²

2R² = 676 · 2

R² = 676

R = 26

Радиус окружности, описанной около треугольника равен 26 ед.

2 Способ.

Если знаете теорему синусов, то можем решить данную задачу с ее помощью.

• Стороны треугольника пропорциональны синусам противолежащих углов.
• Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу окружности, описанной около треугольника.

В нашем случае:

$\displaystyle \frac{AB}{sin\angle{C}} =2R$

По формуле приведения:

sin 135° = sin (180° - 45°) = sin 45° = √2/2

$\displaystyle 2R=\frac{26\sqrt{2}\cdot2 }{\sqrt{2} } \\\\2R=52\\\\R = 26$

Радиус окружности, описанной около треугольника равен 26 ед.

#SPJ1