Question

Вычислите объем тела образованного вращением вокруг оси OY фигуры ограниченной линиями x^2=8y y=3 y=0

Answer 1

Ответ:

объем тела равен  $\boldsymbol {36\pi }$

Пошаговое объяснение:

Формула для вычисления фигуры образованной вращением вокруг оси ОУ

$\displaystyle V=\pi \int\limits^a_b {x^2(y)} \, dy$

У нас все границы известны.

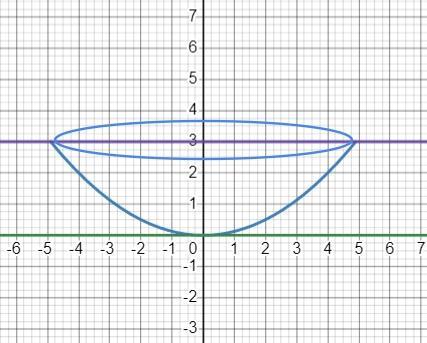
Рисуем график, видим нашу "чашу". считаем.

Тогда у нас будет

$\displaystyle V=\pi \int\limits^3_0 {8y} \, d1yx =\pi *8*\frac{y^2}{2} \bigg |_0^3=\pi \bigg (4*3^2-4*0^2\bigg )=36\pi$

#SPJ1