Предмет: Математика,
автор: Demanaize
Вычислить интеграл: (с подробным решением)
Приложения:
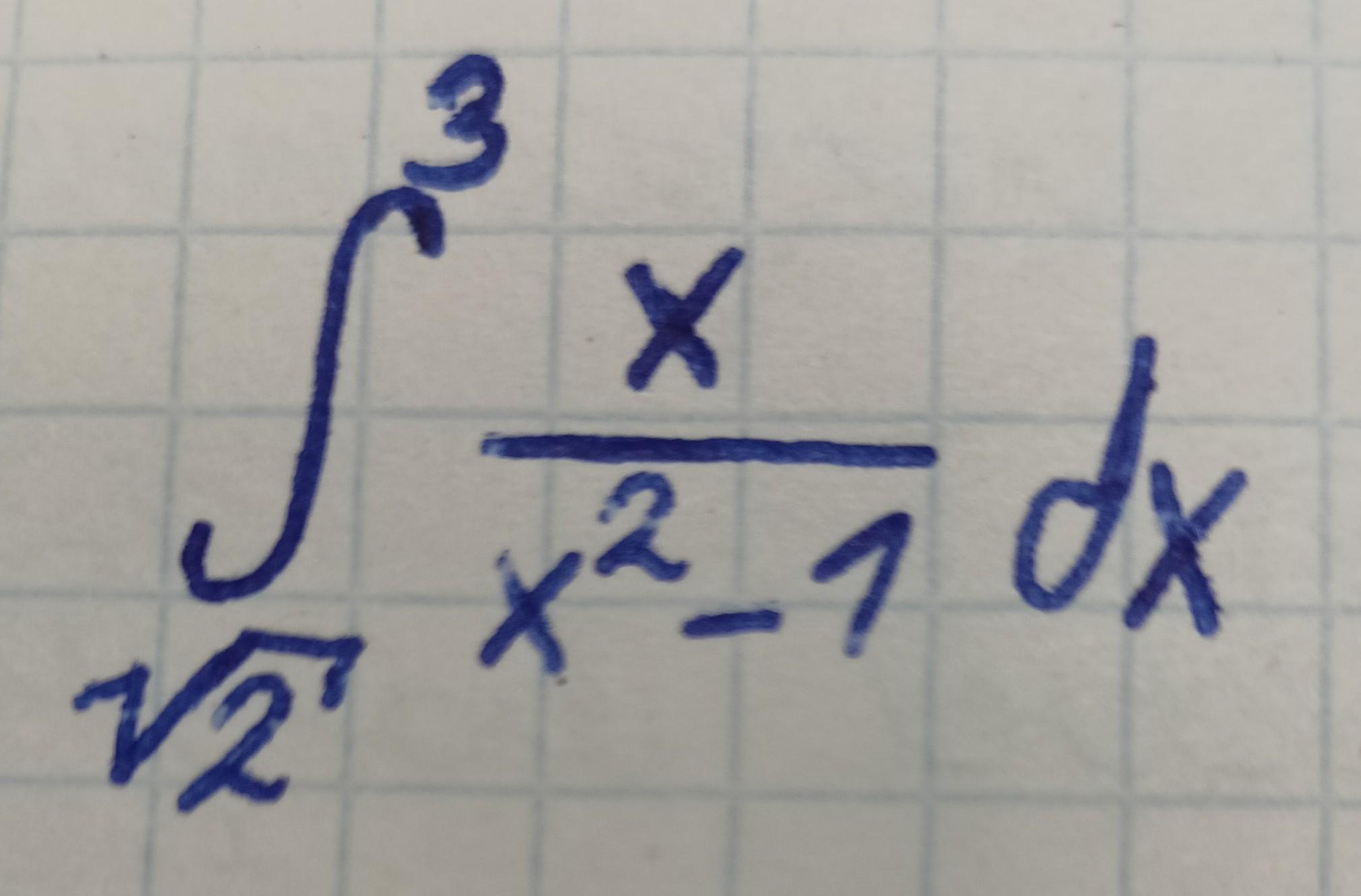
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Пусть х²-1 = у, тогда 2x*dx = dy
Вернёмся к замене
Demanaize:
спасибо огромное!
Похожие вопросы
Предмет: Английский язык,
автор: juldiz82
Предмет: Русский язык,
автор: lizka951400
Предмет: Русский язык,
автор: znatoko228
Предмет: Математика,
автор: Aman2008
Предмет: Русский язык,
автор: artem9112