Предмет: Алгебра,
автор: ajtzanamusina
помогите решить пожалуйстааа!!!
Приложения:
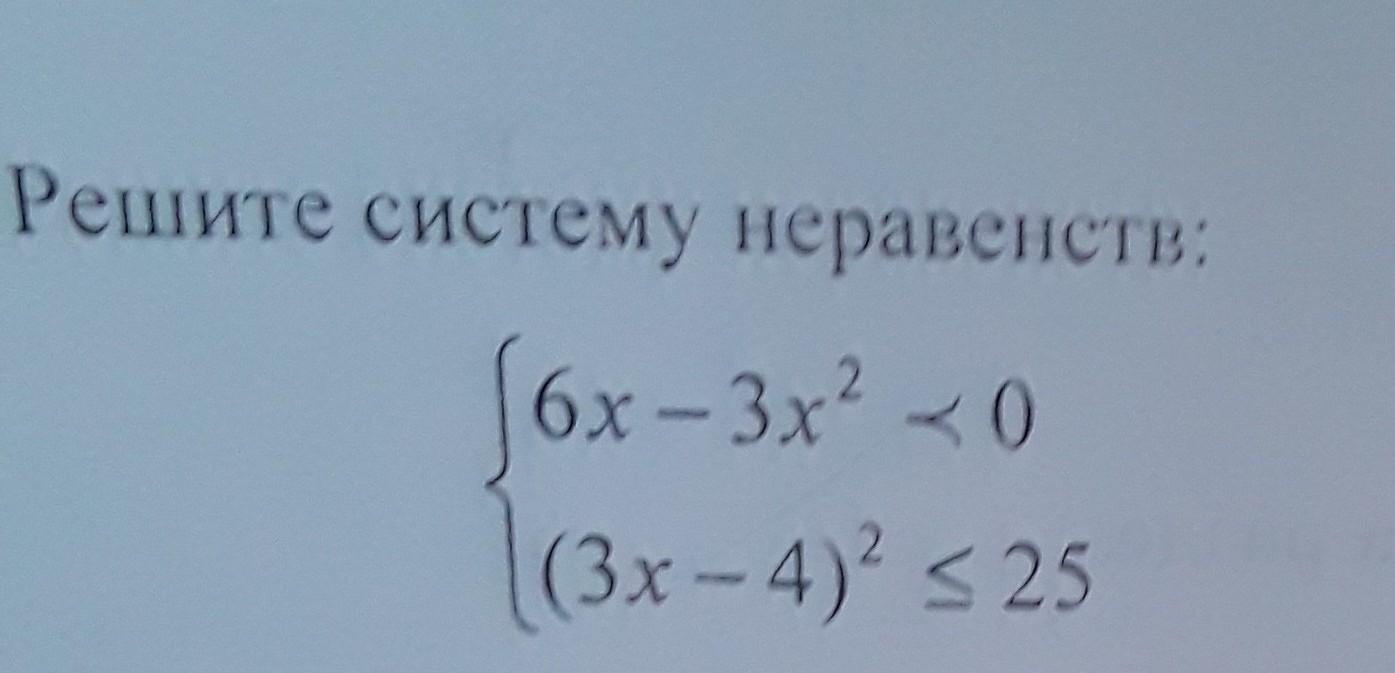
Ответы
Автор ответа:
2
Ответ:
x ∈ ∪
Объяснение:
→ ← → ←
_____-1/3____0____2____3______
x ∈ ∪
6yTep6pog:
пожалуйста Помогите по Алгебре
Автор ответа:
2
Ответ:
Объяснение:
Отобразим на интервале
После объедения промежутков выходит :
пожалуйста Помогите по Алгебре
Похожие вопросы
Предмет: Қазақ тiлi,
автор: 12345678910111234567
Предмет: Окружающий мир,
автор: русский132
Предмет: Қазақ тiлi,
автор: Dalbagan
Предмет: Математика,
автор: zulfiyaalyakhunova
Предмет: Алгебра,
автор: 1415886k