Предмет: Геометрия,
автор: Fantomas22
Помогите решить задачу,даю 52 бала!!
Задача 1
Приложения:
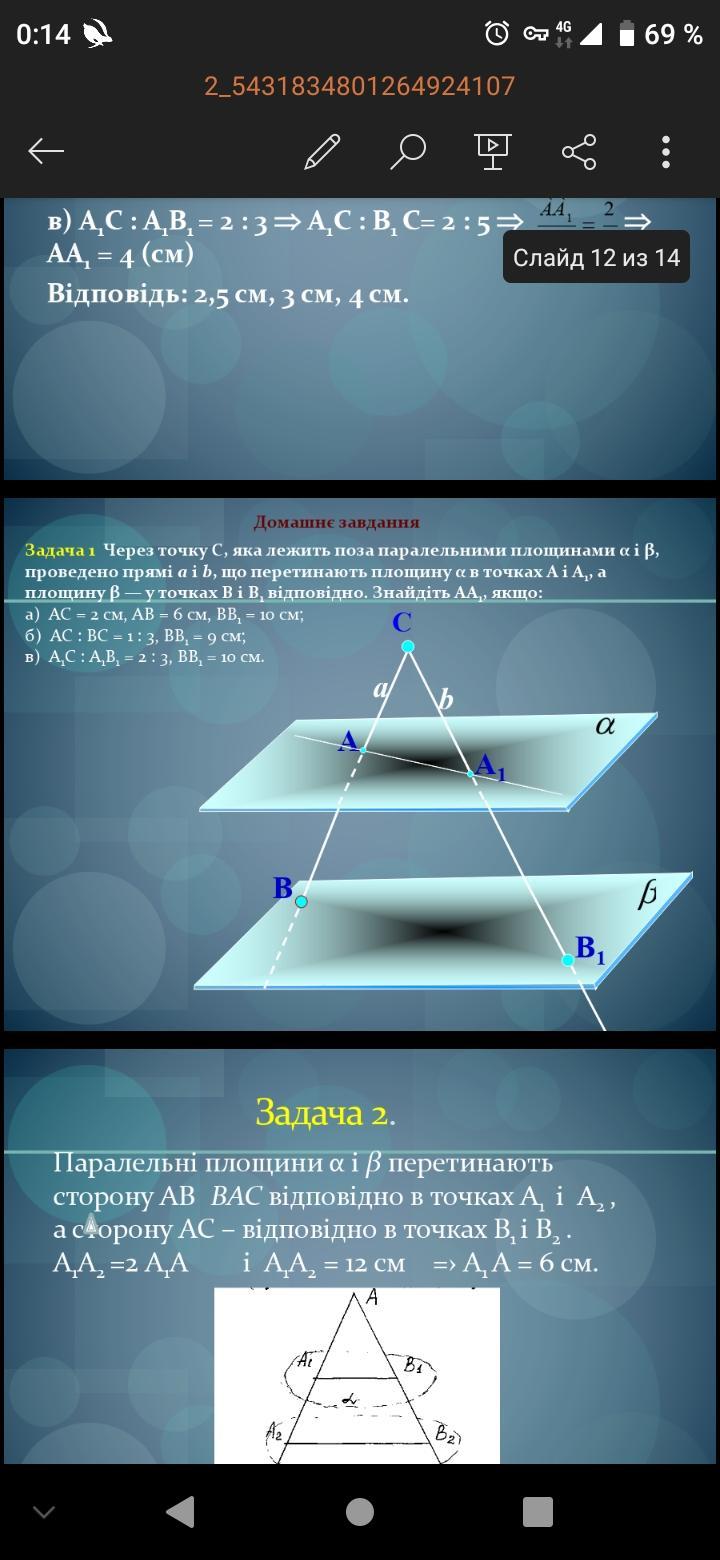
Ответы
Автор ответа:
1
Ответ:
а) 2,5
б) 3
в) 4
Объяснение:
Треугольники CAA1, CBB1 подобны, так как прямая AA1 параллельна прямой BB1 (один угол общий, остальные равны как углы при параллельных прямых). Поэтому:
Пункт а):
б)
в)
Из подобия можно выписать другое отношение:
Похожие вопросы
Предмет: Русский язык,
автор: Tamer2006
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: бек35
Предмет: География,
автор: HiDeNGS
Предмет: Химия,
автор: AlisaVilort