Question

- Имеются два сплава золота и серебра. В одном сплаве эти металлы представлены в соотношении 2:3, а в другом определённые количества данных сплавов и, переплавив их без потерь, в соотношении 3:7. Взяли определенное колличество данных сплавов и, переправили их без потерь, получили 8кг нового слава, в котором масса золота и серебра соотносяться, как 5:11. Какие количества исходных сплавов были взяты?(с решением)​

Answer 1

Ответ:

Количество первого сплава 1 кг.

Количество второго сплава7 кг.

Пошаговое объяснение:

Как я поняла задание:

- Имеются два сплава золота и серебра. В одном сплаве эти металлы представлены в соотношении 2:3, а в другом в соотношении 3:7. Взяли определенное количество данных сплавов и, переправили их без потерь, получили 8 кг нового слава, в котором масса золота и серебра соотносятся, как 5:11. Какие количества исходных сплавов были взяты?

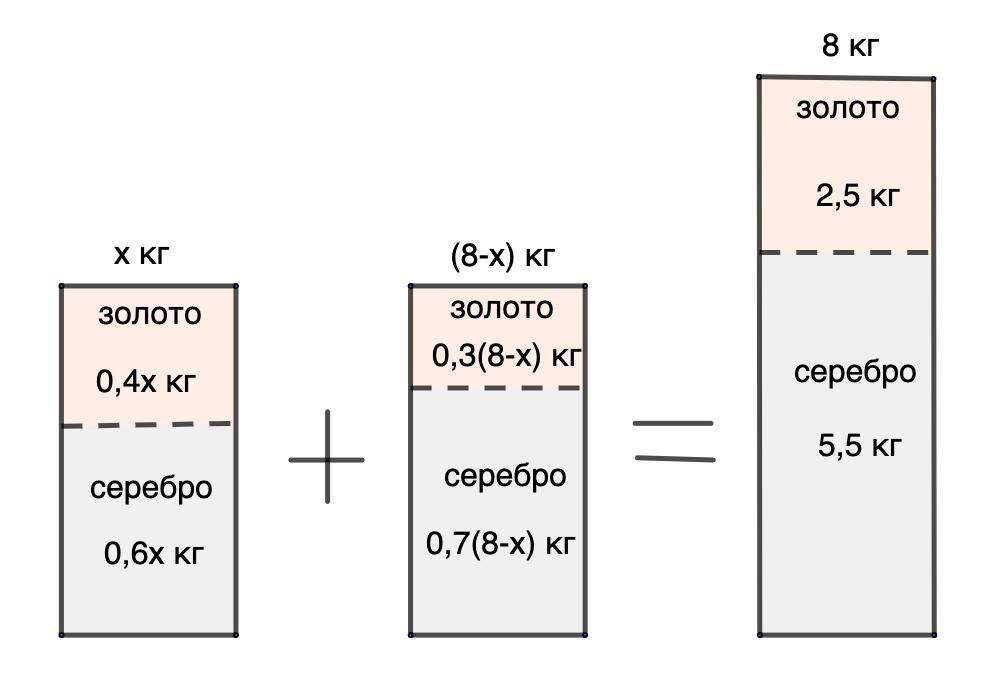
Пусть вес первого сплава - х кг.

Золото : серебро = 2 : 3.

Значит, золота в нем две части из пяти, а серебра - три части из пяти.

• Часть от числа находится умножением.

То есть,

золото -  $\displaystyle \frac{2}{5}\;x$  кг  или  0,4х кг;

серебро - $\displaystyle \frac{3}{5}\;x$  кг  или 0,6х кг.

Вес нового сплава 8 кг.

Следовательно, вес второго сплава равен (8 - х) кг.

Золото : серебро = 3 : 7.

Значит, золота в нем три части из десяти, а серебра - семь частей из десяти.

То есть,

золото -  0,3х кг;

серебро -  0,7х кг.

В новом сплаве весом 8 кг:

Золото : серебро = 5 : 11

Значит, золота в нем пять частей из шестнадцати, а серебра - одиннадцать частей из шестнадцати.

То есть,

золото -  $\displaystyle \frac{5}{16}\cdot8=\frac{5}{2}=2,5$ (кг);

серебро -  $\displaystyle \frac{11}{16}\cdot8=\frac{11}{2}=5,5$ (кг);

Можем составить уравнение либо относительно золота, либо относительно серебра.

Возьмем золото.

0,4х + 0,3 (8 - х) = 2,5

0,4 + 2,4 - 0,3х = 2,5

0,1х = 0,1    |:0,1

х = 1

Получили вес первого сплава 1 кг.

Вес второго сплава: (8 - 1) = 7 кг.