Предмет: Математика,
автор: TemaMama12
Найти частные производные
срочно !
Приложения:
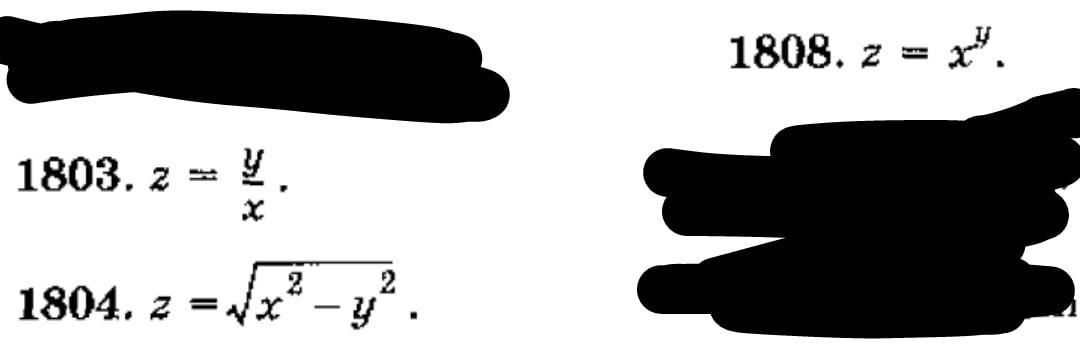
Ответы
Автор ответа:
1
Ответ:
При нахождении частной производной по одной переменной, остальные переменные считаются константами.
Похожие вопросы
Предмет: Английский язык,
автор: va2lenMashenka
Предмет: Другие предметы,
автор: sovaKsunasve
Предмет: Английский язык,
автор: ильнараильнара
Предмет: Химия,
автор: nocomments24