Предмет: Алгебра,
автор: meliodasd526
помогите,дам много баллов.
Приложения:
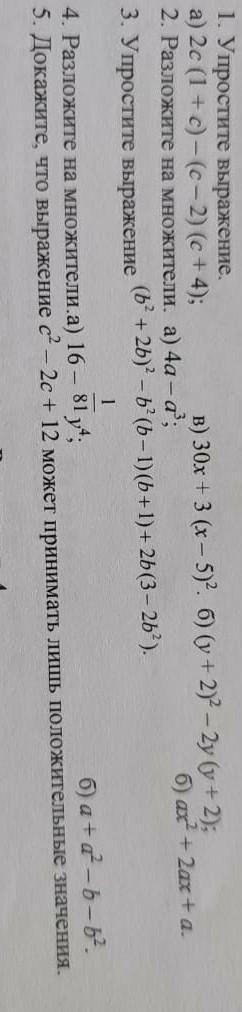
Ответы
Автор ответа:
1
Решение:
1. Упрощаем выражения
2. Раскладываем на множители
3. Упрощаем выражения
4. Снова раскладываем на множители
5. Доказательство
Мы знаем, что квадрат числа, а именно всегда неотрицательный, а тут мы к нему прибавили положительное число
, значит он точно больше 0.
unknownx0:
На будущее: лучше разбивать на несколько заданий
Похожие вопросы
Предмет: Английский язык,
автор: tsifrovoyvek
Предмет: Українська література,
автор: яна1286
Предмет: Окружающий мир,
автор: MarchZh
Предмет: Литература,
автор: vashishina31082006