Предмет: Алгебра,
автор: chipipi
Помогите пожалуйста!!!
Приложения:
Ответы
Автор ответа:
4
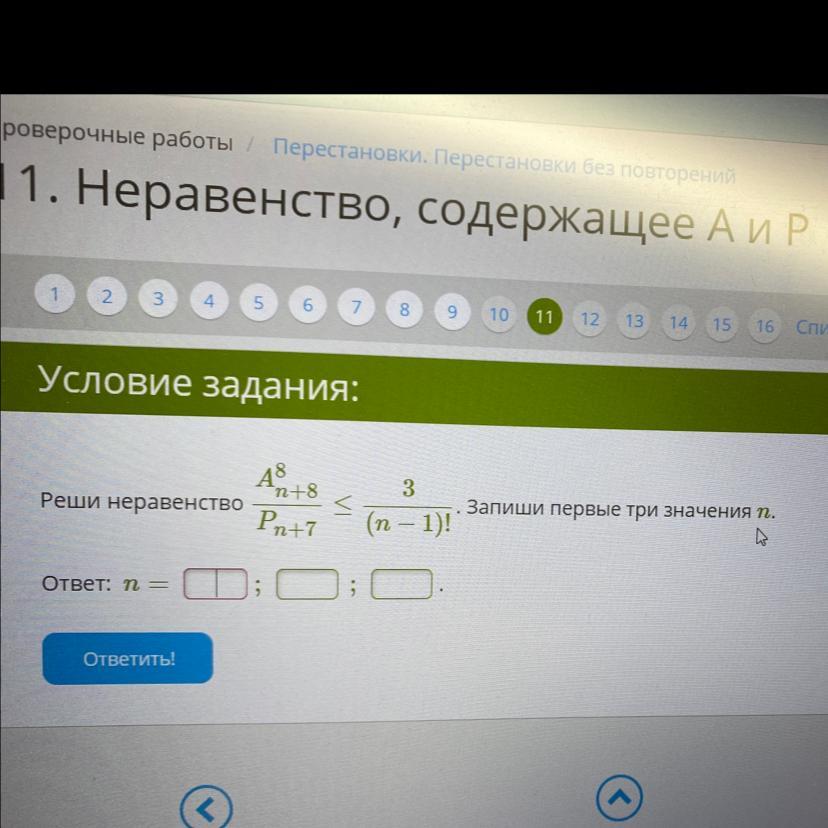
Ответ: n = 4 ; 5 ; 6
Объяснение:
Тогда
n = 4 ; 5 ; 6
Похожие вопросы
Предмет: Русский язык,
автор: Shatunova1976
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: maksimatyrad
Предмет: Русский язык,
автор: Ааа5678
Предмет: Математика,
автор: ez4gg