Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:
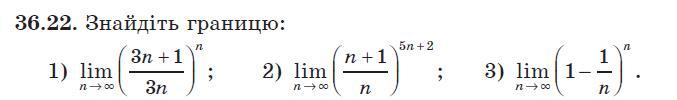
Ответы
Автор ответа:
1
Ответ:
Пределы:
1)
2)
3)
Примечание:
- второй замечательный предел
Объяснение:
1)
2)
Рассмотрим предел , так как
, тогда
.
3)
.
Похожие вопросы
Предмет: Русский язык,
автор: valikhanov
Предмет: Русский язык,
автор: slusarev2009
Предмет: Другие предметы,
автор: Наташа44493940302
Предмет: Українська мова,
автор: diana97788