Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:
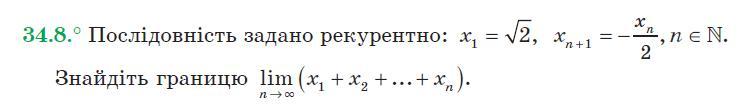
Ответы
Автор ответа:
1
Ответ:
Примечание:
Сумма бесконечно убывающей геометрической прогрессии:
Объяснение:
Вычислим несколько элементов данной последовательности:
Можно сделать гипотезу, что последовательность является бесконечно убывающей геометрической прогрессией.
Вычислим предполагаемые и
, то есть соответственно первый элемент прогрессии и её знаменатель.
По условию:
По определению знаменателя геометрической последовательности:
Так как , то по определению данная последовательность бесконечно убывающая геометрическая прогрессия, по определению, так как по формуле предыдущий элемент отличается на
согласно формуле
.
Бесконечно убывающая геометрическая прогрессия:
Сумма бесконечно убывающей геометрической прогрессии:
.
Похожие вопросы
Предмет: Русский язык,
автор: slusarev2009
Предмет: Другие предметы,
автор: Наташа44493940302
Предмет: Русский язык,
автор: огонь18
Предмет: Русский язык,
автор: aquael262
Предмет: Математика,
автор: Маркк1