Предмет: Математика,
автор: musinskijvladislav9
Розв‘яжіть рівняння 2 і 3 завдання
Приложения:
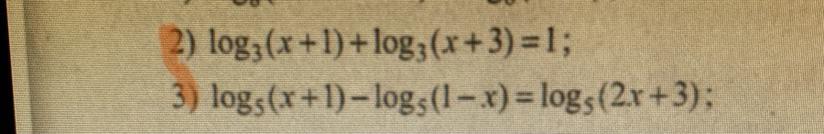
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: SuperShkolnik228
Предмет: Английский язык,
автор: Новичек82
Предмет: Қазақ тiлi,
автор: АринкаЛогвинова
Предмет: Химия,
автор: vicysikk
Предмет: Математика,
автор: VafaMurad1