Найти множества
Помогите 3 задание
Только подробно и понятно..
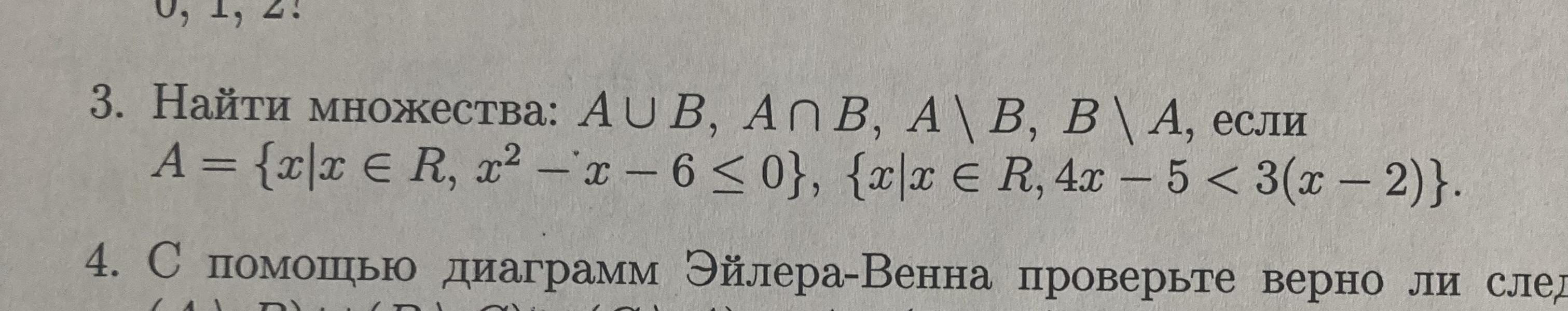
Ответы
Ответ:
Пошаговое объяснение:
A={x| x∈R, x²-x-6≤0}
B={x| x∈R, 4x-5<3(x-2)}
1) Сначала разберемся с какими множествами мы "имеем дело":
Множество А - множество всех действительных решений неравенства x²-x-6≤0
y=x²-x-6 - приведенное квадратное уравнение (коэффициент при х² равен 1). Находим корни по т. Виета:
x₁*x₂=-6 и x₁+x₂=1. Значит, x₁=-2 и x₂=3
x²-x-6 = (x+2)(x-3)
(x+2)(x-3) ≤ 0
Данное неравенство решаем методом интервалов:
+ - +
_______[-2] \\\\\\\\\\\ [3]__________
Значит, множество А= [-2;3]
Множество В - множество всех действительных решений неравенства 4x-5<3(x-2). Решим его:
4x-5 < 3(x-2)
4x-5 < 3x-6
4x-3x < -6+5
x < -1
/////////////////////////// (-1)__________________
Значит, множество B =(-∞;-1)
2) Теперь, ответим на вопросы задачи:
A ∪ B - объединение множеств А и В, т.е. все элементы (значения), которые входят в множество А и множество В:
A ∪ B = (-∞;3]
A ∩ B - пересечение множеств А и В, т.е. элементы (значения), которые являются общими для множеств А и В:
A ∩ B = [-2;-1)
A \ B - все элементы множества А, за исключением элементов множества В:
A \ B = (-1; 3]
B \ A - все элементы множества B, за исключением элементов множества A:
B \ A = (-∞;-2)