Предмет: Математика,
автор: lesnikovnikita65
Доказать, что определенный интеграл равен нулю.
Приложения:
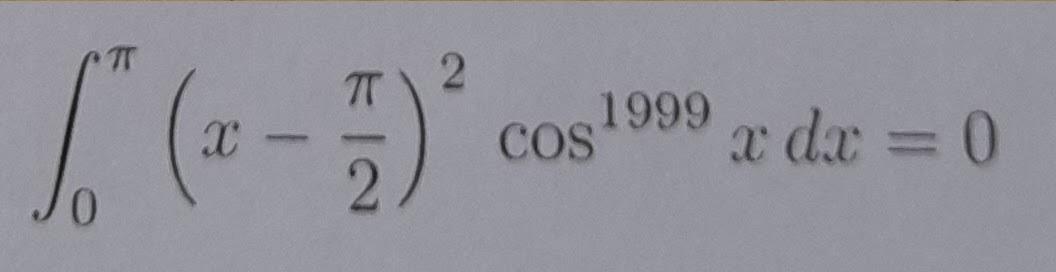
Ответы
Автор ответа:
1
Например: int(-a, a)f(x)dx=int(-a,0)f(x)dx+int(0,a)f(x)dx;
В первом инт-ле делаем замену x= - y; dx = -dy, после чего этот инт-л принимает вид:
int(a,0)f(-y)(-dy)= - int(0, a)[ - f(y)(-dy)= - int(0,a)f(y)dy - то есть первый отличается от второго инт-ла только знаком, а след-но, их сумма =0.
или же:
Точкой х=0 разбейте отрезок на два (тем самым интеграл разбивается на сумму двух интегралов) и воспользуйтесь тем свойством нечётной функции, что f(-x) = -f(x).
Похожие вопросы
Предмет: Русский язык,
автор: itelman96
Предмет: Русский язык,
автор: Алина11657
Предмет: Английский язык,
автор: LauraCattison
Предмет: Химия,
автор: colordarkperson