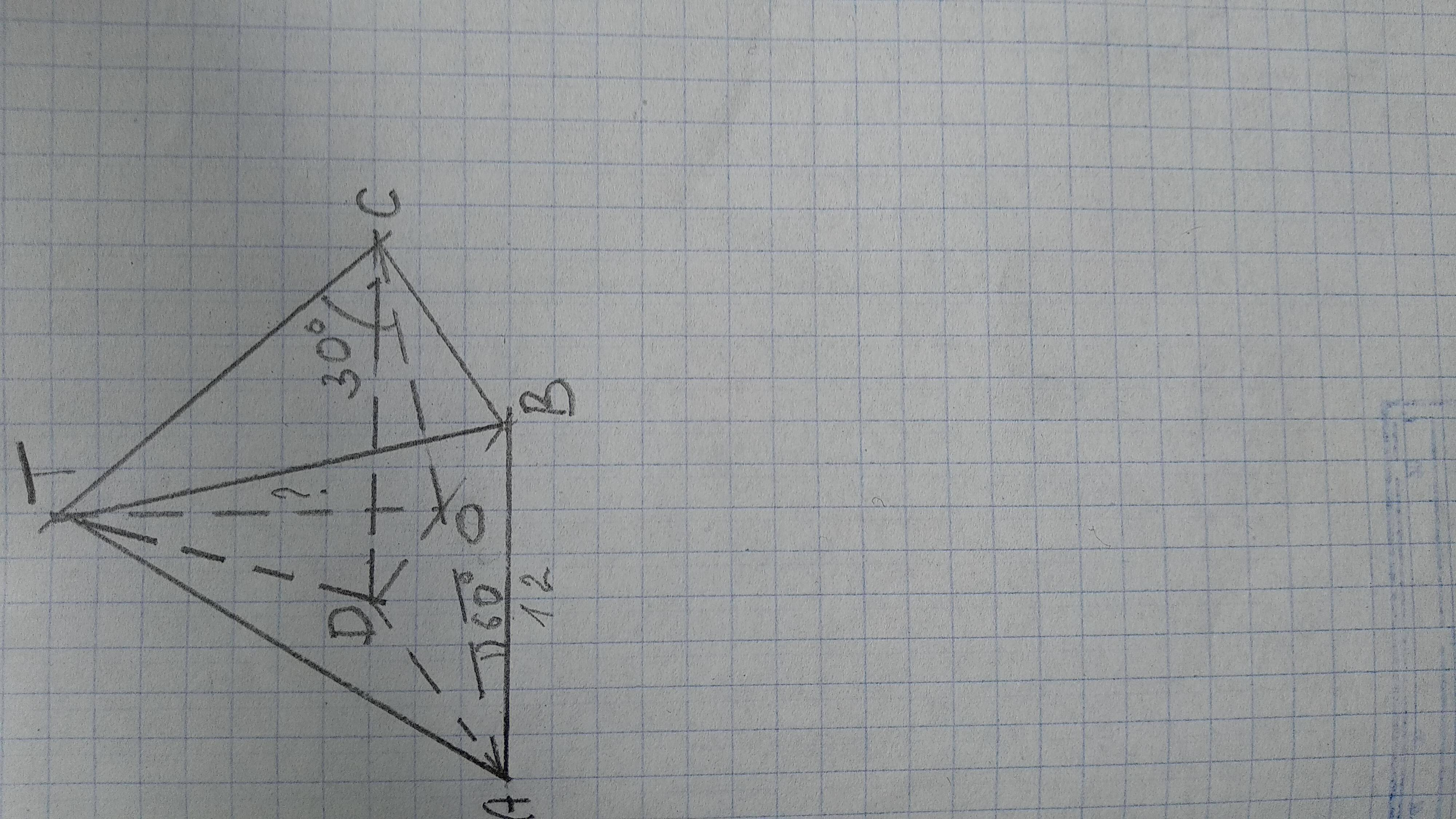Основою піраміди є прямокутник, одна зі сторiн якого дорівнює 12 см і утворює з діагоналлю цього прямокутника кут 60°. Кожне бічне ребро піраміди утворює з площиною основи кут 30°. Знайдіть висоту піраміди. 11:22
Ответы
Ответ:
4√3 см
Объяснение:
Дана пирамида, в основании прямоугольник АВСD, АВ=12 см, ∠САВ=60°;
Т.к. все боковые ребра наклонены к плоскости основания под одним и тем же углом, то вершина пирамиды проектируется в центр окружности, описанной около прямоугольника , т.к. в точку О. Нужно найти ТО, если ТС, ТВ, ТА И ТD наклонено к плоскости основания под углом 30°.
ОС, ОВ, ОА, ОD - соответственно проекции наклонных ТС, ТВ, ТА И ТD на плоскость основания, поэтому углы наклона ∠ТСО=∠ТВО=ТАО=∠ТDО=30°, из ΔТОС(∠О=90°;∠С=30°)
искомая ТО=ОС*tg30°
Задача свелась к нахождению половины диагонали АС, а диагонали в прямоугольнике равны, поэтому из прямоугольного ΔАСВ (∠А=60°, АВ=12см) найдем гипотенузу АС, АС=АВ/cos60°=
12/(1/2)=24(см), половина АС равна ОС=24/2=12(см);
ТО=ОС*tg30°=12*√3/3=4√3(см)