Предмет: Математика,
автор: usiewusow2oq
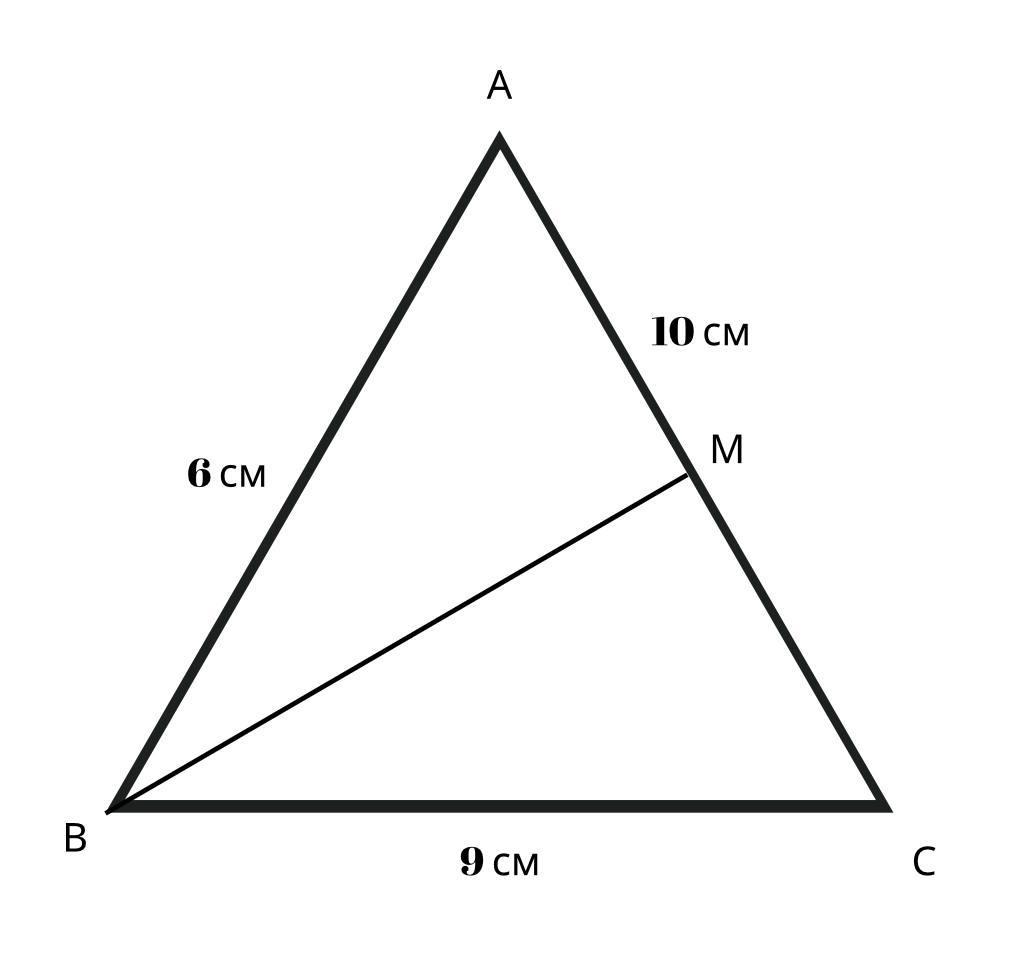
В треугольнике АВС биссектриса ВМ пересекает сторону АС в точке М. Найдите АМ, если стороны АВ=6см, ВС=9см и АС=10см
Приложения:

Ответы
Автор ответа:
0
Ответ:
2 см
Пошаговое объяснение:
Биссектриcа BM делит противолежащую сторону AC на отрезки, пропорциональные прилежащим сторонам (по теореме о биссектрисе угла), т.е.
Введем коэффициент пропорциональности х, тогда АМ=2х см; МС = 3х см; АС= 10 см
Составляем и решаем уравнение:
2х+3х=10
5х=10
х=10/5
х=2
Т.е. АС=2 см.
Ответ: 2 см
Приложения:
iosiffinikov:
Вот всё верно до "Т.е. АС=2 см. Ответ: 2 см". х=2, АМ=2х=4. И спрашивается АМ , а не АС (которое дано).
Спасибо, в ночи решала; проглядела
тем боле, что там даже не АС 2 см, а коэффициент пропорции
и поправить не даёт((
Автор ответа:
0
Ответ:
С) 4 см
Пошаговое объяснение:
По свойству биссектрисы сторона АС делится точкой М в отношении длин сторон ВА и ВС. Пусть АМ=6х , а ВМ=9х. Тогда
6х+9х=10 15х=10 х=2/3 Значит АМ=6*2/3=4 см
Похожие вопросы
Предмет: Русский язык,
автор: Ктотооченьтупой
Предмет: Українська мова,
автор: 0972064059
Предмет: Русский язык,
автор: abeldinova85
Предмет: Информатика,
автор: yriipatalah
Предмет: Русский язык,
автор: ayanwaxbazova