Question

Помогите решить пожалуйста

Answer 1

Ответ:

$\dfrac{\pi}{4}$

Объяснение:

Введем систему координат так, чтобы левая нижняя вершина многоугольника стала началом координат, ось OX направим направо, ось OY - вверх, единица масштаба - длина стороны клеточки. Обозначим вершины:  A(0;0), B(2;6), C(2;2), D(4;5), E(3;2), F(5;4), G(3;1).

Рассмотрим дополнительно точки H(2;0), K(4;2), L(5;2), M(5;1).

Из прямоугольного треугольника ABH тангенс угла B равен

                            $\dfrac{AH}{BH}=\dfrac{2}{6}=\dfrac{1}{3}.$

Поэтому угол B равен арктангенсу одной третьей.

Угол D равен разности углов CDK и EDK (первый равен арктангенсу двух третьих, второй - арктангенсу одной третьей.

Угол F равен разности углов EFL и GFM (первый равен арктангенсу единицы, второй - арктангенсу двух третьих.

Сложив эти углы, получаем ответ.

Замечание. Сделав задачу, начинаешь думать, нельзя ли получить ответ проще и нагляднее. В данном случае это удается сделать. Для этого достаточно углы B, D и F с помощью параллельного переноса перенести в одну точку, скажем, в точку D. При этом сторона BA первого угла пойдет по стороне DE, а сторона BC - по отрезку DK; сторона FG третьего угла пойдет по стороне DC, а сторона FE - по отрезку DN (приходится ввести в рассмотрение еще одну точку - точку N(2;3)). В результате сумма углов, вершины которых отмечены на рисунке точками, равна углу KDN, то есть сорока пяти градусам.  

Answer 2

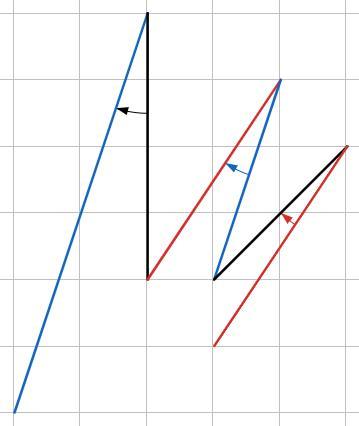
Задача решается визуально, если увидеть две пары параллельных отрезков (синие и красные). Черный отрезок совершает поворот на три искомых угла. Угол между черными отрезками 45°.