Предмет: Алгебра,
автор: tvinkakkscam2
Помощь пожалуйста срочно
Приложения:
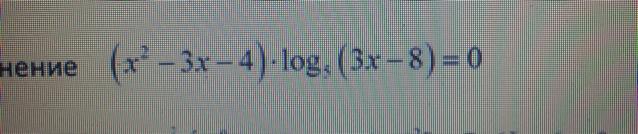
Ответы
Автор ответа:
1
Ответ:
Ответ: 3; 4.
Объяснение:
Решить уравнение:
Число логарифма положительно.
ОДЗ:
- Произведение равно нулю, если хотя бы один из множителей равен нулю.
1)
x₂ не подходит по ОДЗ.
2)
Ответ: 3; 4.
Похожие вопросы
Предмет: Русский язык,
автор: Дима14881488
Предмет: Русский язык,
автор: Ekaterina84113268
Предмет: Другие предметы,
автор: Viki241
Предмет: Русский язык,
автор: nikita4174