Question

СРОЧНО ГЕОМЕТРИЯ
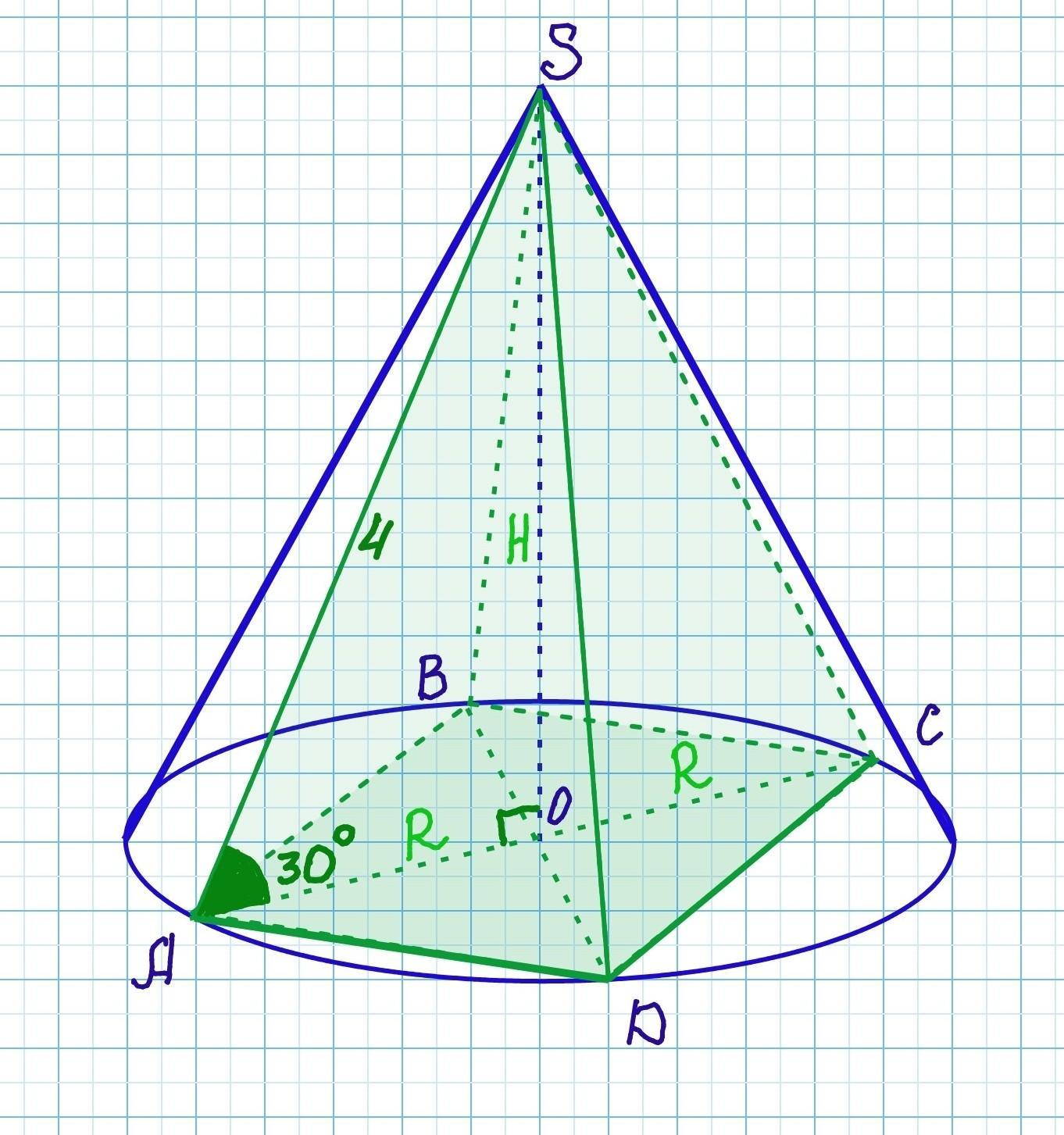
задан конус в который вписана правильная четырехугольная пирамида SABCD.Образующая конуса SA равна 4 и наклонена к плоскости основания под углом 30 градусов. Найдите объем конуса.

Answer 1

Задан конус, в который вписана правильная четырехугольная пирамида SABCD.Образующая конуса SA равна 4 и наклонена к плоскости основания под углом 30 градусов. Найдите объем конуса.

Ответ:

Объем конуса равен $8\pi$ед³

Объяснение:

• Пирамидой, вписанной в конус, называют такую пирамиду, у которой основание вписано в основание конуса, а вершина совпадает с вершиной конуса.

Очевидно, что боковые ребра пирамиды будут равны образующей конуса, то есть равны между собой. Высота пирамиды равна высоте конуса.

• Основанием правильной четырехугольной пирамиды является квадрат.

Вершина конуса проектируется в центр своего основания. Так как она должна совпасть с вершиной пирамиды, то вершина пирамиды проектируется в центр вписанной в основание окружности, что для правильной пирамиды всегда верно.

РЕШЕНИЕ

Имеем правильную четырехугольную пирамиду SABCD, у которой длина бокового ребра SA=SB=SC=SD=4 ед.

В основе пирамиды лежит правильный четырехугольник (т.е. квадрат) ABCD, который вписан в основание конуса.  Поэтому центр окружности, точка O, находится на пересечении диагоналей AC и BD квадрата ABCD. 

Поэтому R=AO – радиус описанной вокруг квадрата окружности и радиус основания конуса, а угол ∠SAO = 30° – угол наклона бокового ребра к плоскости основания.

Рассмотрим прямоугольный треугольник AOS (∠AOS=90°), в котором SA=4– гипотенуза,

∠SAO=30°– угол прилегающий к катету AO=R и противоположный катету SO=H.

Известно, что катет, лежащий напротив угла в 30° равен половине гипотенузы, поэтому:

SO=H=½•SA=½•4=2 ед

 По определению косинуса острого угла прямоугольного треугольника найдем прилегающий AO = R – радиус основания:

AO=R=SA•cos∠SAO=4•cos30°=4•√3/2= 2√3 ед

 

 Вычислим объем заданного конуса:

$V= \frac{1}{3} \pi {R}^{2} H = \frac{1}{3}\pi \times{(2 \sqrt{3})}^{2} \times 2 = 8 \pi$см³

#SPJ1