Предмет: Геометрия,
автор: rafloulait
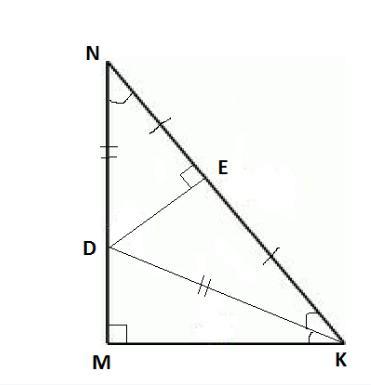
В прямоугольном треугольнике MNK с гипотенузой NK проведены биссектриса KD и перпендикуляр DE к гипотенузе. Докажите, что если MN = 3MD,
то NE =EK.
Ответы
Автор ответа:
1
Объяснение:
ΔMDK = ΔEDK - по II признаку (∠DEK = ∠DMK; ∠EKD = ∠DKM; DK - общая сторона) ⇒ МК=ЕК
MN=3MD ⇒ DN = 2MD
Биссектриcа KD делит противолежащую сторону MN на отрезки, пропорциональные прилежащим сторонам (по теореме о биссектрисе угла), т.е.
⇒
MK=EK ⇒ NK = 2EK
NK = NE+ЕК ⇒ NE + EK = 2EK ⇒ NE = EK
Что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ТИРГРИЦА
Предмет: Русский язык,
автор: ЛеРоЧкАкРаВчУк
Предмет: Английский язык,
автор: nxizhnyakova
Предмет: Математика,
автор: 7363116
Предмет: Математика,
автор: Rimma66