Предмет: Математика,
автор: K1ngMan228
Найти производную (с помощью формул и правил сложения, умножения, частного)
Приложения:
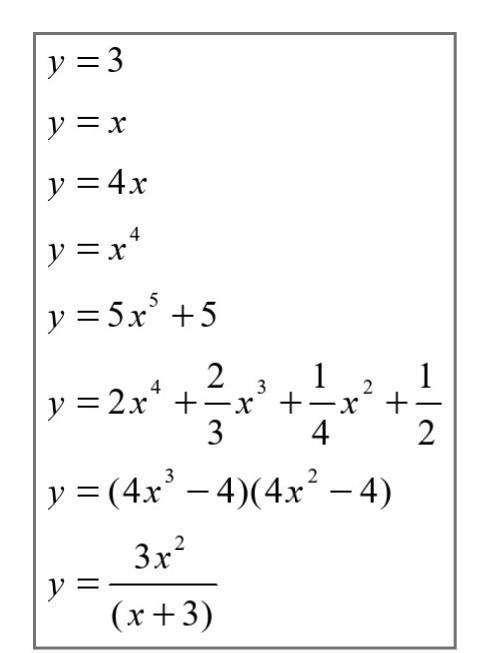
Ответы
Автор ответа:
0
Формулы для решения:
Похожие вопросы
Предмет: Українська мова,
автор: Ромка255
Предмет: Русский язык,
автор: Аюбжан
Предмет: Английский язык,
автор: Яна11111супер
Предмет: Математика,
автор: kirillzelek