Предмет: Математика,
автор: K1ngMan228
Найти производную (с помощью формул и правил сложения, умножения, частного)
Приложения:
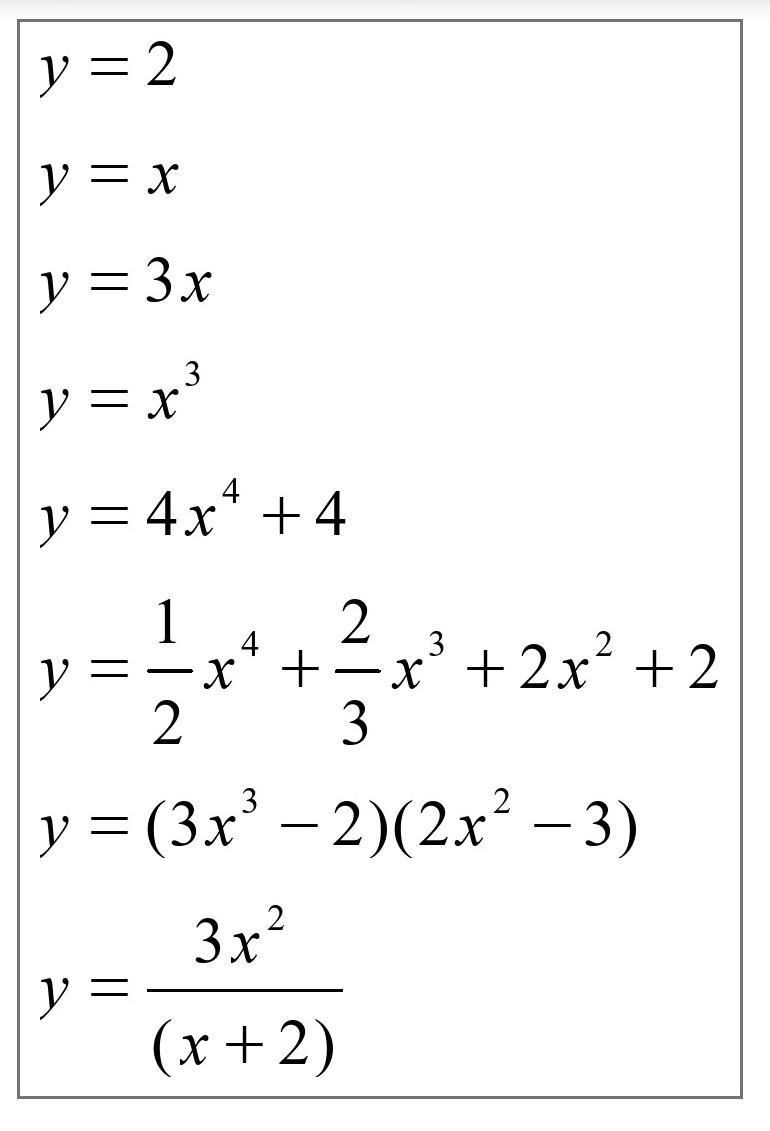
Ответы
Автор ответа:
2
Пошаговое объяснение:
Вспомним формулы
Посчитаем
Автор ответа:
1
Ответ:
y'=0
y'=1
y'=3
y'=3x²
y'=16x³
y'=2x³+2x²+4x
y'=9x²(2x²-3)+4x(3x³-3)
y'=(6x(x+2)-3x²)/(x+2)²
Пошаговое объяснение:
Это не упрощенный вариант ответов. Но они тоже правильные
Похожие вопросы
Предмет: Русский язык,
автор: Mashanyann
Предмет: Русский язык,
автор: карапуз47
Предмет: Английский язык,
автор: kris326
Предмет: Химия,
автор: neslin31
Предмет: Литература,
автор: IIntelectual