Question

ABCD - параллелограмм. Укажите верные утверждения, с решением!​

Answer 1

Ответ:

A), C), F) — верные.

Объяснение:

Удачи.

Answer 2

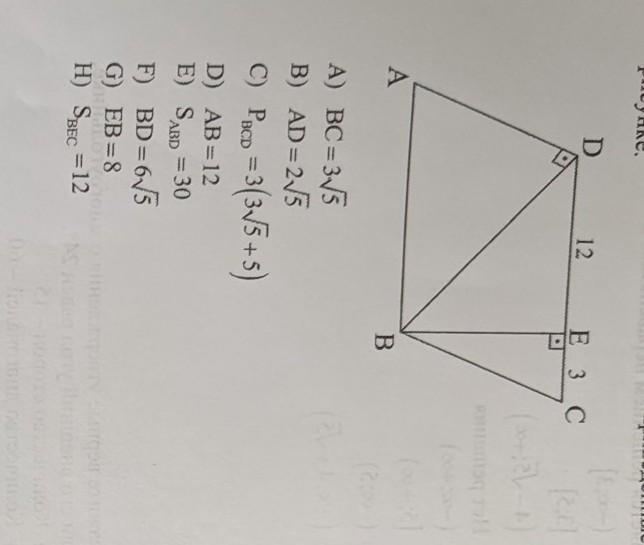
В параллелограмме АВСD ∠ADB=90°,BE⊥DC,DE=12,CE=3. Найти

А)ВС ; В)АD;  С)Р(ВСD) ; D)АВ ; Е)S(ABD) ; F)BD ; G)EB ; Н)S(BEC).

Объяснение:

Тк АВСD-параллелограмм ,

• то ВС||AD,BD-секущая ⇒∠ADB=∠DBC=90° ⇒ΔBDC-прямоугольный;
• то АВ=CD=12+3=15;

А)По среднему геометрическому для катета имеем ВС=√(СЕ*СD)=√(3*15)=3√5 ,верно.

В)AD=BC=3√5, 3√5≠2√5. Неверно.

С)По т.Пифагора из ΔBCD ищем BD =√(15²-(3√5)²)=√180=6√5.

Р(ВСD)=CD+BD+DC=15+6√5+3√5=9√5+15=3(3√5+5) .Верно.

D)АВ=CD=12+3=15. Неверно.

Е)Диагональ параллелограмма делит его на два равновеликих треугольника.S(ABD)=S(BCD)=1/2*CD*BE=1/2*3√5*6√5=45. Неверно.

F)По т.Пифагора из ΔBCD ищем BD =√(15²-(3√5)²)=√180=6√5. Верно.

G)EB-высота прямоугольного ΔBCD. По среднему геометрическому для высоты имеем ЕВ=√(12*3)=6. Неверно.

Н)S(BEC)=1/2*CE*EB=1/2*3*6=9, неверно.