Знайти площу фигури, обмеженої лініями:
xy =3 , y =3+2,
y=1
y=1
Ответы
Ответ:
Пошаговое объяснение:
Строим графики, определяемся с фигурой, пределами интегрирования и по формуле Ньютона-Лейбница ищем площадь фигуры.
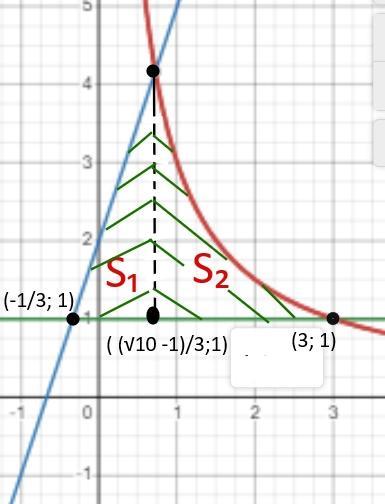
Наша искомая фигура состоит из двух фигур, определяемых двумя функциями. Вот и придется нам искать две площади.
И, более того, по графикам не определяются точные границы.
Поэтому поищем их самостоятельно.
Самая противная средняя граница.
Ищем ее как пересечение графиков функций у = х/3 и у = 3х+2.
Корень х₂ для нас не актуален, он относится к нижней части графика ху=3.
Мы рассматриваем только корень х₁ = ( (√10 -1)/3). - это наш "центральный" предел интегрирования
Самая левая точка интегрирования определяем как пересечение графиков функций у = 1 и у = 3х +2
3х +2 = 1
х = -1/3
Наш "левый" предел интегрирования х₀ = (-1/3)
И с правым совсем просто. х₂ = 3
Ну и вот....
Ищем площадь S1
Теперь ищем площадь S2
И теперь сумма