Предмет: Математика,
автор: cl3n4chn
Если не сложно, решите пожалуйста!
Приложения:
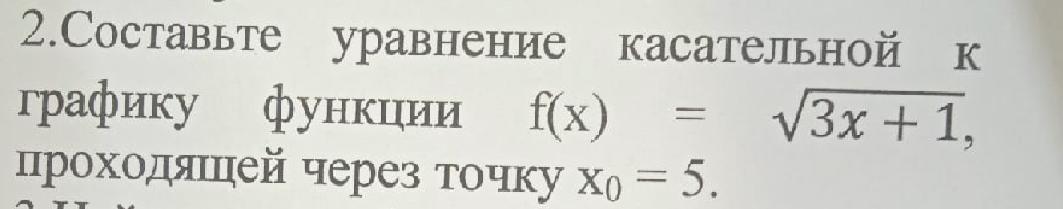
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Уравнение касательной, проходящей через точку записывается так:
Найдем
Далее найдем и
, где
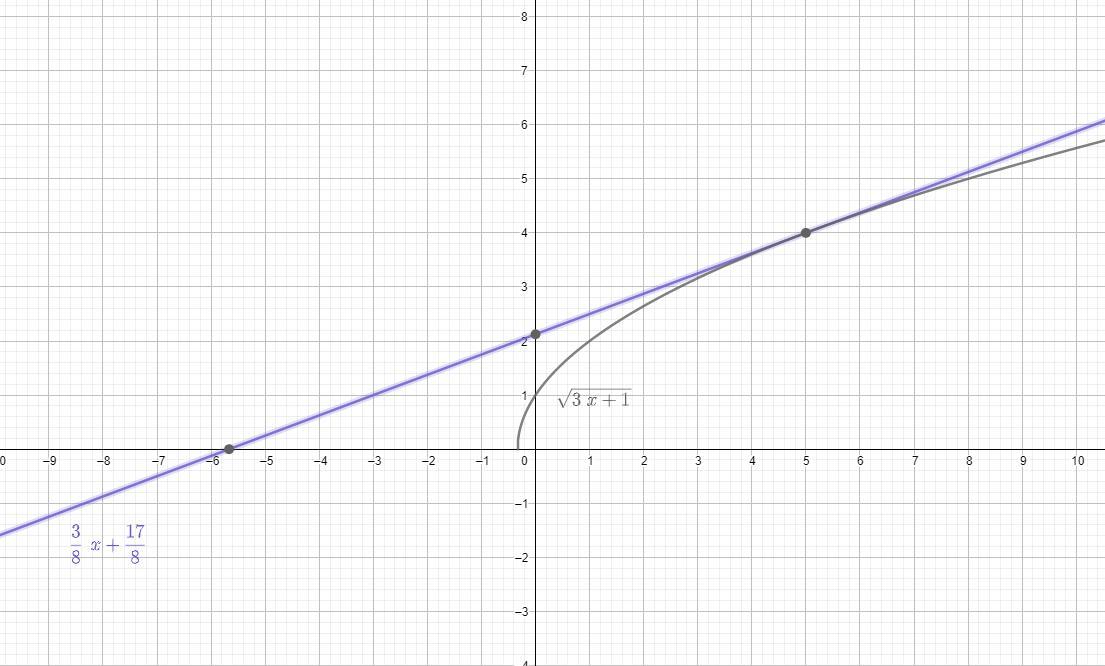
Запишем уравнение касательной
Для наглядности внизу график
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Ksu1217
Предмет: Русский язык,
автор: выделислова
Предмет: Английский язык,
автор: Ручка1111111
Предмет: Русский язык,
автор: damirospanov3644
Предмет: Обществознание,
автор: GBbeketay