Предмет: Математика,
автор: TezAdventure
Найти интеграл.......................
Приложения:
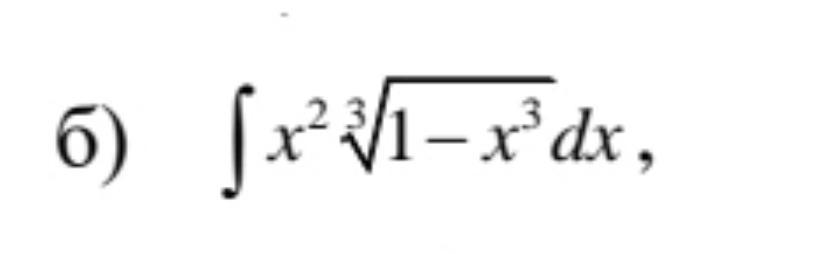
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: RRIX
Предмет: Русский язык,
автор: kokich3
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: kamrantagiev05