Предмет: Геометрия,
автор: girlokay
В прямоугольном треугольнике АВС ( угол С – прямой) произведена высота СН. Радиусы кругов, вписанных в треугольники АСН и ВСН, равны 8 и 15 см. Найдите радиус окружности вписанный в треугольник АВС
Ответы
Автор ответа:
1
Ответ:
Объяснение:
(синие углоки)
(по двум углам - один прямой, другой синий)
Отсюда следует пропорциональность сторон треугольников и радиусо вписаных окружностей.
Обозначим за радиус окружности вписанную в
, и за
и
радиусы окружностей, списаных в треугольники
и
соответсвенно.
Тогда из их подобия следует, что отношение радиуса вписаной окружности к гипотенузе треугольника (маленького или большого) постоянно и равно
.
Запишем теорему Пифагора для
Умножим все на
Выразим (искомый радиус)
Приложения:
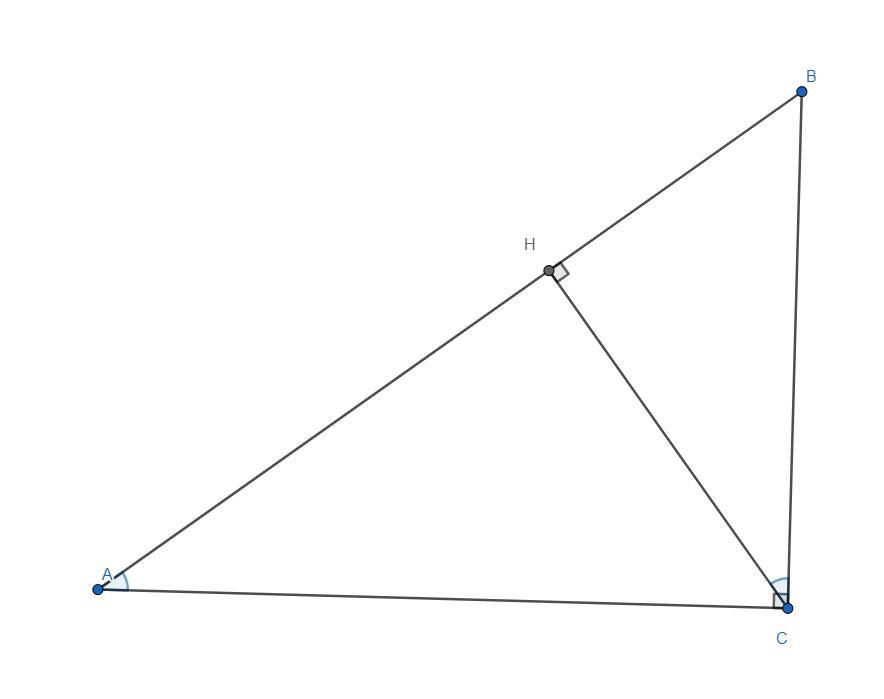
Похожие вопросы
Предмет: Русский язык,
автор: Виталина0101
Предмет: Русский язык,
автор: yankaa51
Предмет: Українська мова,
автор: kapinam9
Предмет: Математика,
автор: theandreaharris