Решите пж фаст 50 баллов спасибки)
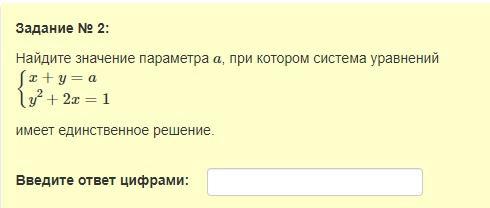
Ответы
Единственное решение - это координаты точки касания прямой
к кривой
Значит, прямая должна быть касательной.
1)
2) Касательная к графику функции имеет одну единственную общую точку с этим графиком.
Производная функции в точке
равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке иначе производная функции
в точке
равна угловому коэффициенту касательной в этой точке.
3)
- угловой коэффициент касательной.
4)
- этот же угловой коэффициент касательной из данного уравнения прямой.
5) Приравняем эти значения и найдём это будет
6) В уравнение подставим
и найдём
.
7) Подставим и
в уравнение
.
Ответ: 1